题目内容
18.函数y=tan($\frac{π}{4}x-\frac{π}{2}$)的部分图象如图所示,则△AOB的面积等于( )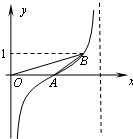
| A. | 1 | B. | 2 | C. | 4 | D. | $\frac{9}{2}$ |
分析 求出函数的周期,即可求出A的坐标,结合三角形的面积公式进行求解即可.
解答 解:函数的周期T=$\frac{π}{\frac{π}{4}}=4$,则A(2,0),
则△AOB的面积S=$\frac{1}{2}×2×1=1$,
故选:A
点评 本题主要考查三角形的面积的计算,根据正切函数的性质求出函数的周期是解决本题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
8.下列说法正确的是( )
| A. | 已知p:?x0∈R,x02+x0-1=0,q:?x∈R,x2+x+1>0,则p∧q是真命题 | |
| B. | 命题p:若$\overrightarrow a⊥\overrightarrow b$,则$\overrightarrow a•\overrightarrow b=0$的否命题是:若$\overrightarrow a⊥\overrightarrow b$,则$\overrightarrow a•\overrightarrow b≠0$ | |
| C. | ?x∈R,x2+x-1<0的否定是?x0∈R,x02+x0-1>0 | |
| D. | x=$\frac{π}{3}$是$y=sin(2x-\frac{π}{6})$取最大值的充要条件 |
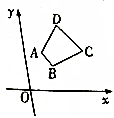 已知梯形ABCD,如图所示,其中AB∥CD,且DC=2AB,三个顶点的坐标分别为A(1,2)、B(2,1)、C(4,2),求点D的坐标.
已知梯形ABCD,如图所示,其中AB∥CD,且DC=2AB,三个顶点的坐标分别为A(1,2)、B(2,1)、C(4,2),求点D的坐标.