题目内容
16.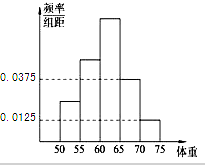 某校为了提高学生的身体素质,决定组建学校足球队,学校为了解学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12.
某校为了提高学生的身体素质,决定组建学校足球队,学校为了解学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12.(1)求该校报名学生的总人数;
(2)从报名的学生中任选3人,设X表示体重超过60kg的学生人数,求X的数学期望.
分析 (1)根据频数关系求出每段的频数即可求该校报名学生的总人数;
(2)X=0,1,2,3,求出每个变量对应的概率,即可得到结论.
解答 解:(1)∵从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12.
∴从左到右3个小组的频数分别为6,12,18,共有36人,
第4,5小组的频率之和为(0.0375+0.0125)×5=0.25,
则前3小组的频率之和为1-0.25=0.75,
则该校报名学生的总人数为36÷0.75=48;
(2)第4,5小组的频数为48×0.25=12,
则体重超过60kg的学生人数为12+18=30,
则X=0,1,2,3,
则P(X=0)=$\frac{{C}_{18}^{3}}{{C}_{48}^{3}}$=$\frac{51}{1081}$≈0.047,P(X=1)=$\frac{{C}_{18}^{2}{C}_{30}^{1}}{{C}_{48}^{3}}$=≈0.265,
P(X=2)=$\frac{{C}_{18}^{1}{C}_{30}^{2}}{{C}_{48}^{3}}$≈0.453,P(X=3)=$\frac{{C}_{30}^{3}}{{C}_{48}^{3}}$=$\frac{1015}{4324}$≈0.235,
则EX=0×0.047+1×0.265+2×0.453+3×0.235=1.876,
即X的数学期望EX=1.876
点评 本题主要考查概率和统计的应用,以及随机变量的期望的计算,求出每个变量的概率是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.设等差数列{an}满足$\frac{si{n}^{2}{a}_{4}-co{s}^{2}{a}_{4}+co{s}^{2}{a}_{4}co{s}^{2}{a}_{8}-si{n}^{2}{a}_{4}si{n}^{2}{a}_{8}}{sin({a}_{5}+{a}_{7})}$=1,公差d∈(-1,0),若当且仅当n=9时,数列{an}的前n项和Sn取得最大值,则首项a1的取值范围是( )
| A. | (π,$\frac{9π}{8}$) | B. | [π,$\frac{9π}{8}$] | C. | [$\frac{7π}{6}$,$\frac{4π}{3}$] | D. | ($\frac{7π}{6}$,$\frac{4π}{3}$) |
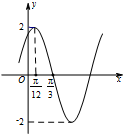 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.