��Ŀ����
4�� ��֪��ԲC��$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��{a��b��0}��$�����ҽ���ֱ���F1��-c��0����F2��c��0����ֱ��l��x=my-c����ԲC���ڵ�M��N���㣬��m=-$\frac{{\sqrt{3}}}{3}$��M����ԲC�Ķ��㣬�ҡ�MF1F2���ܳ�Ϊ6��
��֪��ԲC��$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��{a��b��0}��$�����ҽ���ֱ���F1��-c��0����F2��c��0����ֱ��l��x=my-c����ԲC���ڵ�M��N���㣬��m=-$\frac{{\sqrt{3}}}{3}$��M����ԲC�Ķ��㣬�ҡ�MF1F2���ܳ�Ϊ6����1������ԲC�ķ��̣�
��2����M��F2��N��ֱ��x=4�ϵ���Ӱ�ֱ�ΪE��K��D������MD����m�仯ʱ��֤��ֱ��MD��NE�ཻ��һ���㣬������ö�������ꣻ
��3������ԲC����ΪA��ֱ��AM��AN��ֱ��x=4�ֱ��ཻ�ڵ�P��Q�����ʣ���m�仯ʱ�����߶�PQΪֱ����Բ��x��صõ��ҳ��Ƿ�Ϊ��ֵ�����ǣ���������ֵ�������ǣ���˵�����ɣ�
���� ��1����m=-$\frac{{\sqrt{3}}}{3}$ʱ���ɵ�ֱ��l����б��Ϊ$\frac{2��}{3}$���������й���a��c�ķ����飬���a��c��ֵ����������������b������ԲC�ķ��̿���
��2���ɣ�1�����c=1����ֱ��l�ķ���Ϊx=my+1������ֱ�߷��̺���Բ���̣���Ϊ����y��һԪ���η��̣����ø���ϵ���Ĺ�ϵ�õ�M��N��������ĺ������
Ȼ������ֱ��l��x�ᴹֱʱ��MD��NE�Ľ���ΪG��$\frac{5}{2}��0$����������б�����֤��MG������G��$\frac{5}{2}��0$����NEҲ������G��$\frac{5}{2}��0$��������˵��ֱ��MD��NE�ཻ��һ���㣬�ö��������ΪG��$\frac{5}{2}��0$����
��3�����ֱ��AM�ķ��̣��õ�P�����꣬ͬ���ɵ�Q���꣬��H��x��y��Ϊ��PQΪֱ����Բ������һ�㣬�ɵ�$\overrightarrow{PH}•\overrightarrow{QH}=0$���õ���PQΪֱ����Բ�ķ���ȡy=0�����x=1��x=7��˵����PQΪֱ����Բ�����1��0���루7��0��������m�仯ʱ�����߶�PQΪֱ����Բ��x��صõ��ҳ��Ƕ�ֵ6��
��� ��1���⣺��m=-$\frac{{\sqrt{3}}}{3}$ʱ��ֱ��l����б��Ϊ$\frac{2��}{3}$��
�������$\left\{\begin{array}{l}{2a+2c=6}\\{\frac{c}{a}=cos\frac{��}{3}}\end{array}\right.$�����a=2��c=1��b=$\sqrt{3}$��
����ԲC�ķ���Ϊ$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$��
��2���ɣ�1��֪��c=1����ֱ��l�ķ���Ϊx=my+1��
��M��x1��y1����N��x2��y2����
��$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{x=my-1}\end{array}\right.$���ɵã�3m2+4��y2+6my-9=0��
��${y}_{1}+{y}_{2}=\frac{-6m}{3{m}^{2}+4}��{y}_{1}{y}_{2}=\frac{-9}{3{m}^{2}+4}$��
��ֱ��l��x�ᴹֱʱ���ɵ�MD��NE�Ľ���ΪF2K���е�G��$\frac{5}{2}��0$����
��ֱ��l��x���ֱʱ������֤��MD������G��$\frac{5}{2}��0$����
�������֪D��4��y2����
${k}_{GD}=\frac{{y}_{2}}{4-\frac{5}{2}}=\frac{2{y}_{2}}{3}$��${k}_{AG}=\frac{{y}_{1}}{{x}_{1}-\frac{5}{2}}=\frac{{y}_{1}}{m{y}_{1}-\frac{3}{2}}$��
��${k}_{AG}-{k}_{GD}=\frac{{y}_{1}}{m{y}_{1}-\frac{3}{2}}-\frac{2{y}_{2}}{3}$=$\frac{{y}_{1}}{m{y}_{1}-\frac{3}{2}}-\frac{2}{3}•\frac{-9}{��3{m}^{2}+4��{y}_{1}}$
=$\frac{��3{m}^{2}+4��{{y}_{1}}^{2}+6��m{y}_{1}-\frac{3}{2}��}{��m{y}_{1}-\frac{3}{2}����3{m}^{2}+4��{y}_{1}}$=$\frac{��3{m}^{2}+4��{{y}_{1}}^{2}+6m{y}_{1}-9}{��m{y}_{1}-\frac{3}{2}����3{m}^{2}+4��{y}_{1}}=0$��
��kAG=kGD����MG������G��$\frac{5}{2}��0$����
ͬ����֤NEҲ������G��$\frac{5}{2}��0$����
��ֱ��MD��NE�ཻ��һ���㣬�ö��������ΪG��$\frac{5}{2}��0$����
��3��������ɵ�ֱ��AM�ķ���Ϊ$y=\frac{{y}_{1}}{{x}_{1}+2}��x+2��$��
��x=4����P��������$4��\frac{6{y}_{1}}{{x}_{1}+2}$����
ͬ���ɵ�Q��$4��\frac{6{y}_{2}}{{x}_{2}+2}$����
��H��x��y��Ϊ��PQΪֱ����Բ������һ�㣬��$\overrightarrow{PH}•\overrightarrow{QH}=0$��
����PQΪֱ����Բ�ķ���Ϊ$��x-4��^{2}+��y-\frac{6{y}_{1}}{{x}_{1}+2}����y-\frac{6{y}_{2}}{{x}_{2}+2}��=0$��
��y=0����$��x-4��^{2}+\frac{36{y}_{1}{y}_{2}}{��m{y}_{1}+3����m{y}_{2}+3��}=0$��
��$��x-4��^{2}+\frac{36{y}_{1}{y}_{2}}{{m}^{2}{y}_{1}{y}_{2}+3m��{y}_{1}+{y}_{2}��+9}=0$��
��$��x-4��^{2}+\frac{36��\frac{-9}{3{m}^{2}+4}}{{m}^{2}��\frac{-9}{3{m}^{2}+4}+3m��\frac{-6m}{3{m}^{2}+4}+9}=0$��
��$��x-4��^{2}+\frac{-9��36}{-9{m}^{2}-18{m}^{2}+27{m}^{2}+36}=0$��
����x-4��2=9�����x=1��x=7��
����PQΪֱ����Բ�����1��0���루7��0����
�൱m�仯ʱ�����߶�PQΪֱ����Բ��x��صõ��ҳ��Ƕ�ֵ6��
���� ���⿼����Բ���̵���������ֱ������Բ��λ�ù�ϵ��Ӧ�ã�ѵ��������б��֤�����㹲�����⣬������Բ�ķ��̵�Ӧ�ã�ֱ�����������������÷��̵ĸ���ϵ���Ĺ�ϵ��⣬�Ǵ��������������Ϊ���õķ�������Բ���ߵ��ص��Ǽ������Ƚϴ�Ҫ�����߱���ǿ��������������������ѹ���⣮

 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д� ��ͨ����ͬ����ϰ��ϵ�д�
��ͨ����ͬ����ϰ��ϵ�д�| A�� | 2035 | B�� | 2036 | C�� | 4084 | D�� | 4085 |
| A�� | $\frac{��}{6}�ܦȡ�\frac{��}{2}$ | B�� | $\frac{��}{3}�ܦȡ�\frac{��}{2}$ | C�� | $0�ܦȡ�\frac{��}{3}$ | D�� | $0���ȣ�\frac{2��}{3}$ |
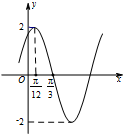 ��֪����f��x��=Asin����x+�գ���A��0���أ�0��|��|��$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ��
��֪����f��x��=Asin����x+�գ���A��0���أ�0��|��|��$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ��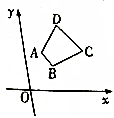 ��֪����ABCD����ͼ��ʾ������AB��CD����DC=2AB���������������ֱ�ΪA��1��2����B��2��1����C��4��2�������D�����꣮
��֪����ABCD����ͼ��ʾ������AB��CD����DC=2AB���������������ֱ�ΪA��1��2����B��2��1����C��4��2�������D�����꣮