题目内容
13．
如图，在△ABC中，已知点D在BC边上，cos∠ADC=$\frac{\sqrt{2}}{3}$，cos∠BAD=$\frac{\sqrt{3}}{3}$，AD=2，则BA的长为（ ）| A． | $\frac{14\sqrt{3}+4\sqrt{21}}{3}$ | B． | 7$\sqrt{3}$+4 | C． | $\sqrt{3}$+4$\sqrt{7}$ | D． | 7+4$\sqrt{7}$ |
分析 先计算sin∠B，再在△ABD中，由正弦定理可得AB．
解答 解：由题意，cos∠ADB=-$\frac{\sqrt{2}}{3}$，sin∠ADB=$\frac{\sqrt{7}}{3}$，sin∠BAD=$\frac{\sqrt{6}}{3}$
sin∠B=sin（∠BAD+∠ADB）=$\frac{\sqrt{6}}{3}•（-\frac{\sqrt{2}}{3}）+\frac{\sqrt{3}}{3}•\frac{\sqrt{7}}{3}$=$\frac{\sqrt{21}-\sqrt{12}}{9}$，
△ABD中，由正弦定理可得$\frac{2}{\frac{\sqrt{21}-\sqrt{12}}{9}}=\frac{AB}{\frac{\sqrt{7}}{3}}$，
∴AB=$\frac{14\sqrt{3}+4\sqrt{21}}{3}$，
故选：A．
点评 本题考查解三角形，考查正弦定理，比较基础．
练习册系列答案
相关题目
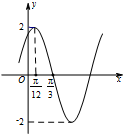已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示．