题目内容
19.定义:曲线C上的点到点P的距离的最小值称为曲线C到点P的距离.已知曲线C:y=$\frac{1}{x}$(x>0)到点P(a,a)的距离为$\frac{3\sqrt{2}}{2}$,则实数a的值为-$\frac{1}{2}$或$\frac{\sqrt{26}}{2}$.分析 分P在曲线C外部和内部两种情况求解,当P在曲线外部时,直接由两点间的距离求解,当P在曲线内部时,写出以P(a,a)为圆心,以$\frac{3\sqrt{2}}{2}$为半径的圆的方程,再设圆与曲线的公共弦方程为y=-x+b,联立直线与曲线、直线与圆,求得交点坐标,由坐标相等求得a的值.
解答 解:当P在曲线C外部时,P到曲线的最小值为P到(1,1)的距离,
等于$\sqrt{2(a-1)^{2}}=\frac{3\sqrt{2}}{2}$,解得a=-$\frac{1}{2}$或a=$\frac{5}{2}$(舍);
当P在曲线C内部时,以P(a,a)为圆心,以$\frac{3\sqrt{2}}{2}$为半径的圆为$(x-a)^{2}+(y-a)^{2}=\frac{9}{2}$.
设曲线y=$\frac{1}{x}$(x>0)与圆$(x-a)^{2}+(y-a)^{2}=\frac{9}{2}$的公共弦所在直线方程为y=-x+b,
联立$\left\{\begin{array}{l}{y=-x+b}\\{y=\frac{1}{x}}\end{array}\right.$,得x2-bx+1=0,解得${x}_{1}=\frac{b-\sqrt{{b}^{2}-4}}{2}$(靠近y轴交点横坐标).
联立$\left\{\begin{array}{l}{y=-x+b}\\{(x-a)^{2}+(y-a)^{2}=\frac{9}{2}}\end{array}\right.$,得4x2-4bx+4a2+2b2-4ab-9=0.
解得:${x}_{2}=\frac{b-\sqrt{4ab+9-4{a}^{2}-{b}^{2}}}{2}$(靠近y轴交点横坐标).
由x1=x2,得$\sqrt{{b}^{2}-4}=\sqrt{4ab+9-4{a}^{2}-{b}^{2}}$,即b2-4=4ab+9-4a2-b2,
∴4a2-4ab+2b2=13.
设直线y=-x+b交x轴于A,交y轴于B,由对称性及四边形内角和为360°可知a=b,
∴4a2-4a2+2a2=13,解得$a=-\frac{\sqrt{26}}{2}$(舍)或$a=\frac{\sqrt{26}}{2}$.
故答案为:-$\frac{1}{2}$或$\frac{\sqrt{26}}{2}$.
点评 本题考查直线与圆锥曲线的位置关系,考查了圆与圆锥曲线的位置关系,考查了学生的理解能力和运算能力,是中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 已知p:?x0∈R,x02+x0-1=0,q:?x∈R,x2+x+1>0,则p∧q是真命题 | |
| B. | 命题p:若$\overrightarrow a⊥\overrightarrow b$,则$\overrightarrow a•\overrightarrow b=0$的否命题是:若$\overrightarrow a⊥\overrightarrow b$,则$\overrightarrow a•\overrightarrow b≠0$ | |
| C. | ?x∈R,x2+x-1<0的否定是?x0∈R,x02+x0-1>0 | |
| D. | x=$\frac{π}{3}$是$y=sin(2x-\frac{π}{6})$取最大值的充要条件 |
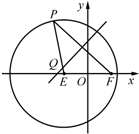 如图,已知圆E:${(x+\sqrt{3})^2}+{y^2}$=16,点$F(\sqrt{3},0)$,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
如图,已知圆E:${(x+\sqrt{3})^2}+{y^2}$=16,点$F(\sqrt{3},0)$,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.