题目内容
16．已知函数f（x）=$lo{g}_{\frac{1}{2}}（3+2x-{x}^{2}）$，则f（x）的值域是[-2，+∞）．分析 先分析内函数y=3+2x-x2的图象和性质，进而得到最大值，再由外函数是减函数，得到答案．
解答 解：∵函数y=3+2x-x2的图象是开口朝下，且以直线x=1为对称轴的抛物线，
故当x=1时，函数取最大值4，
故当x=1时，函数f（x）=$lo{g}_{\frac{1}{2}}（3+2x-{x}^{2}）$取最小值-2，无最大值，
故f（x）的值域是[-2，+∞），
故答案为：[-2，+∞）．
点评 本题考查的知识点是对数函数的图象和性质，复合函数的单调性，难度中档．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
11．已知函数$f（x）=\frac{4x}{{3{x^2}+3}}$，函数$g（x）=\frac{1}{3}a{x^3}-{a^2}x（a≠0）$，若对任意x1∈[0，2]，总存在x2∈[0，2]，使f（x1）=g（x2），则实数a的取值范围是（ ）
| A． | （0，+∞） | B． | $[\frac{1}{3}，1]$ | C． | $[\frac{1}{3}，+∞）$ | D． | （0，1] |
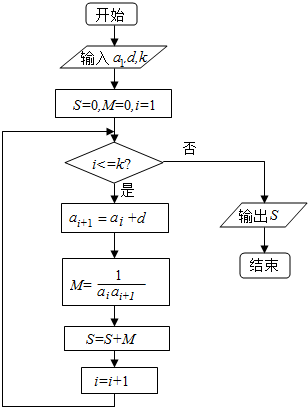已知数列{an}的各项均为正数，观察程序框图