题目内容
10.设函数f(x)为二次函数,且满足下列条件:①f(x)≤f($\frac{1-2a}{2}$)(a∈R);②当x1<x2,x1+x2=0时,有f(x1)>f(x2).则实数a的取值范围是( )| A. | a>$\frac{1}{2}$ | B. | a≥$\frac{1}{2}$ | C. | a≤$\frac{1}{2}$ | D. | a<$\frac{1}{2}$ |
分析 根据条件可知函数有函数f(x)由最大值,即开口向下,f(x)的对称轴x<0,继而求出a的范围.
解答 解:函数f(x)为二次函数,且满足下列条件:①f(x)≤f($\frac{1-2a}{2}$)(a∈R);
∴函数f(x)由最大值,即开口向下,
由②当x1<x2,x1+x2=0时,有f(x1)>f(x2),可知f(x)的对称轴x<0,
∴$\frac{1-2a}{2}$<0,
解得a>$\frac{1}{2}$,
故选:A.
点评 本题考查了函数图象的识别,以及二次函数的性质,属于基础题.

练习册系列答案
相关题目
19.如图,在三角形ABC中,已知AB=2,AC=3,∠BAC=θ,点D为BC的三等分点.则$\overrightarrow{AD}•\overrightarrow{BC}$的取值范围为( )

| A. | $({-\frac{11}{3},\frac{13}{3}})$ | B. | $({\frac{1}{3},\;\frac{7}{3}})$ | C. | $({-\frac{5}{3},\frac{55}{3}})$ | D. | $({-\frac{5}{3},\;\frac{7}{3}})$ |
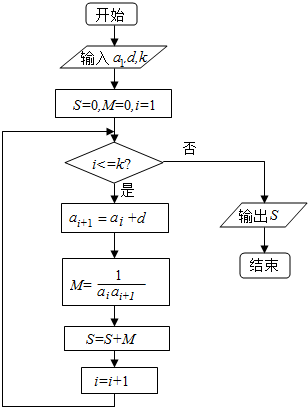 已知数列{an}的各项均为正数,观察程序框图
已知数列{an}的各项均为正数,观察程序框图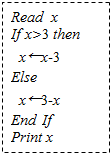 如图是一个算法的伪代码,若输入x的值为1,则输出的x的值是2.
如图是一个算法的伪代码,若输入x的值为1,则输出的x的值是2.