题目内容
11.设定义在R上的奇函数f(x)的导函数是f′(x),当x≠0,f′(x)+$\frac{f(x)}{x}$>0,若a=2f(2),b=$\frac{1}{3}f(\frac{1}{3}),c=ln3f(ln3)$,比较a,b,c的大小( )| A. | c<b<a | B. | c<a<b | C. | b<c<a | D. | a<b<c |
分析 由题意构造g(x)=xf(x),求出g′(x),化简已知的式子判断出g′(x)的符号,可得g(x)在(0,+∞)上的单调性,由函数的单调性可判断出a、b、c的大小关系.
解答 解:设g(x)=xf(x),则g′(x)=f(x)+xf′(x),
因为当x≠0,f′(x)+$\frac{f(x)}{x}$>0,
所以$\frac{xf′(x)+f(x)}{x}>0$,
则当x>0时,f(x)+xf′(x)>0,即g′(x)>0,
所以函数g(x)在(0,+∞)上递增,
因为$0<\frac{1}{3}<ln3<2$,所以$g(\frac{1}{3})<g(ln3)<g(2)$,
则$\frac{1}{3}f(\frac{1}{3})<ln3f(ln3)<2f(2)$,即b<c<a,
故选:C.
点评 本题考查函数的单调性与导数的关系,以及构造函数法,属于中档题.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
19.如图,在三角形ABC中,已知AB=2,AC=3,∠BAC=θ,点D为BC的三等分点.则$\overrightarrow{AD}•\overrightarrow{BC}$的取值范围为( )

| A. | $({-\frac{11}{3},\frac{13}{3}})$ | B. | $({\frac{1}{3},\;\frac{7}{3}})$ | C. | $({-\frac{5}{3},\frac{55}{3}})$ | D. | $({-\frac{5}{3},\;\frac{7}{3}})$ |
3.已知集合A={x|y=log2x,y<0},$B=\left\{{y\left|{y={{(\frac{1}{2})}^x},0<x<1}\right.}\right\}$,则A∪B=( )
| A. | (0,1) | B. | $(\frac{1}{2},+∞)$ | C. | $(\frac{1}{2},1)$ | D. | (-∞,1) |
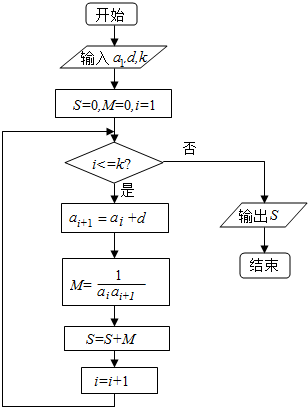 已知数列{an}的各项均为正数,观察程序框图
已知数列{an}的各项均为正数,观察程序框图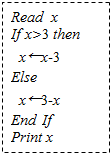 如图是一个算法的伪代码,若输入x的值为1,则输出的x的值是2.
如图是一个算法的伪代码,若输入x的值为1,则输出的x的值是2.