题目内容
9.设函数$f(x)=x+\frac{1}{x}$(1)判断函数的奇偶性;
(2)探究函数y=f(x)在[1,+∞)上的单调性,并用单调性的定义证明.
分析 (1)由解析式求出函数的定义域,化简f(-x)后由函数奇偶性的定义即可判断;
(2)先判断出函数的单调性,再利用函数单调性的定义证明.
解答 解:(1)函数$f(x)=x+\frac{1}{x}$是奇函数,
函数$f(x)=x+\frac{1}{x}$的定义域是{x|x≠0},
因为$f(-x)=-x-\frac{1}{x}$=-f(x),
所以函数f(x)数奇函数;
(2)函数$f(x)=x+\frac{1}{x}$在[1,+∞)上是增函数,
证明:设x1>x2≥1,
则f(x1)-f(x2)=${x}_{1}+\frac{1}{{x}_{1}}$-(${x}_{2}+\frac{1}{{x}_{2}}$)
=(x1-x2)+$\frac{1}{{x}_{1}}-\frac{1}{{x}_{2}}$=(x1-x2)+$\frac{{x}_{2}-{x}_{1}}{{x}_{1}{x}_{2}}$
=(x1-x2)(1-$\frac{1}{{x}_{1}{x}_{2}}$)=$\frac{({x}_{1}-{x}_{2})({x}_{1}{x}_{2}-1)}{{x}_{1}{x}_{2}}$,
∵x1>x2≥1,∴x1-x2>0,x1x2-1>0,x1x2>0,
∴$\frac{({x}_{1}-{x}_{2})({x}_{1}{x}_{2}-1)}{{x}_{1}{x}_{2}}>$0,
∴f(x1)-f(x2)>0,则f(x1)>f(x2),
∴函数$f(x)=x+\frac{1}{x}$在[1,+∞)上是增函数.
点评 本题考查函数的奇偶性、单调性的判断以及证明,考查化简、变形能力,属于中档题.

练习册系列答案
相关题目
16.某皮鞋厂从今年1月份开始投产,并且前4个月的产量分别为如表所示
由于产品质量好,款式新颖,前几个月的产品销售情况良好,为了推销员在推销产品时,按受订单不至于过多或过少,需要估测以后几个月的产量,厂里分析,产量的增加是由于工人生产熟练和理顺了生产流程,厂里也暂时不准备增加设备和工人.如果用x表示月份,用y表示产量,试比较y=a$\sqrt{x}$+b和y=abx+c哪一个更好些?(函数模型y=a$\sqrt{x}$+b,要求用第1、4月份的数据确定a、b,函数模型y=abx+c要求用第1、2、3月份的数据确定a、b、c,精确到0.01,$\sqrt{2}≈1.414$,$\sqrt{3}≈1.732$)
| 月份 | 1 | 2 | 3 | 4 |
| 产量(万双) | 1.02 | 1.10 | 1.16 | 1.18 |
17.实系数一元二次方程x2+ax+2b=0的一个根在(0,1)上,另一个根在(1,2)上,则$\frac{b-3}{a-1}$的取值范围是( )
| A. | [1,3] | B. | (1,3) | C. | $[{\frac{1}{2},\frac{3}{2}}]$ | D. | $({\frac{1}{2},\frac{3}{2}})$ |
19.如图,在三角形ABC中,已知AB=2,AC=3,∠BAC=θ,点D为BC的三等分点.则$\overrightarrow{AD}•\overrightarrow{BC}$的取值范围为( )

| A. | $({-\frac{11}{3},\frac{13}{3}})$ | B. | $({\frac{1}{3},\;\frac{7}{3}})$ | C. | $({-\frac{5}{3},\frac{55}{3}})$ | D. | $({-\frac{5}{3},\;\frac{7}{3}})$ |
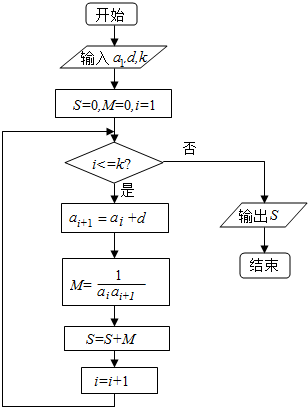 已知数列{an}的各项均为正数,观察程序框图
已知数列{an}的各项均为正数,观察程序框图