题目内容
【题目】已知函数![]() .
.
(1)若![]() ,求证:
,求证:![]() .
.
(2)讨论函数![]() 的极值;
的极值;
(3)是否存在实数![]() ,使得不等式
,使得不等式![]() 在
在![]() 上恒成立?若存在,求出
上恒成立?若存在,求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
【答案】(1)证明见解析;(2)见解析;(3)存在,1.
【解析】
(1)![]() ,求出
,求出![]() 单调区间,进而求出
单调区间,进而求出![]() ,即可证明结论;
,即可证明结论;
(2)对![]() (或
(或![]() )是否恒成立分类讨论,若恒成立,没有极值点,若不恒成立,求出
)是否恒成立分类讨论,若恒成立,没有极值点,若不恒成立,求出![]() 的解,即可求出结论;
的解,即可求出结论;
(3)令![]() ,可证
,可证![]() 恒成立,而
恒成立,而![]() ,由(2)得,
,由(2)得,![]() 在
在![]() 为减函数,
为减函数,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 都存在
都存在![]() ,不满足
,不满足![]() ,当
,当![]() 时,设
时,设![]() ,且
,且![]() ,只需求出
,只需求出![]() 在
在![]() 单调递增时
单调递增时![]() 的取值范围即可.
的取值范围即可.
(1)![]() ,
,![]() ,
,
![]() ,当
,当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,∴
,∴![]() ,故
,故![]() .
.
(2)由题知,![]() ,
,![]() ,
,
①当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减,没有极值;
上单调递减,没有极值;
②当![]() 时,
时,![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
故![]() 在
在![]() 处取得极小值
处取得极小值![]() ,无极大值.
,无极大值.
(3)不妨令![]() ,
,
设![]() 在
在![]() 恒成立,
恒成立,
![]() 在
在![]() 单调递增,
单调递增,![]() ,
,
![]() 在
在![]() 恒成立,
恒成立,
所以,当![]() 时,
时,![]() ,
,
由(2)知,当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
![]() 恒成立;
恒成立;
所以不等式![]() 在
在![]() 上恒成立,只能
上恒成立,只能![]() .
.
当![]() 时,
时,![]() ,由(1)知
,由(1)知![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,不满足题意.
,不满足题意.
当![]() 时,设
时,设![]() ,
,
因为![]() ,所以
,所以![]() ,
,
![]() ,
,
即![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,所以
,所以![]() 时,
时,![]() 恒成立,
恒成立,
即![]() 恒成立,
恒成立,
故存在![]() ,使得不等式
,使得不等式![]() 在
在![]() 上恒成立,
上恒成立,
此时![]() 的最小值是1.
的最小值是1.

【题目】为了响应国家号召,促进垃圾分类,某校组织了高三年级学生参与了“垃圾分类,从我做起”的知识问卷作答随机抽出男女各20名同学的问卷进行打分,作出如图所示的茎叶图,成绩大于70分的为“合格”.
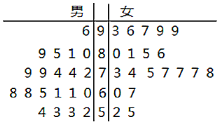
(Ⅰ)由以上数据绘制成2×2联表,是否有95%以上的把握认为“性别”与“问卷结果”有关?
男 | 女 | 总计 | |
合格 | |||
不合格 | |||
总计 |
(Ⅱ)从上述样本中,成绩在60分以下(不含60分)的男女学生问卷中任意选2个,记来自男生的个数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
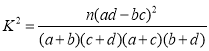
![]()