题目内容
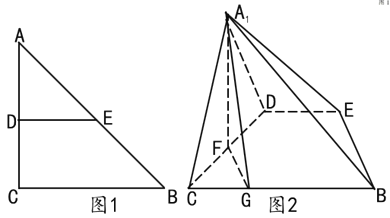
【题目】如图,在六面体ABCDEFG中,平面![]() 平面DEFG,
平面DEFG,![]() 平面DEFC,
平面DEFC,![]() ,
,![]() ,且
,且![]() .
.
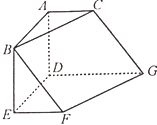
(1)求证:![]() 平面ACGD;
平面ACGD;
(2)若![]() ,求点D到平面GFBC的距离
,求点D到平面GFBC的距离
【答案】(1)证明见解析;(2)![]() .
.
【解析】
![]() 证明
证明![]() ,
,![]() ,得到
,得到![]() 平面DEFG,得到平面
平面DEFG,得到平面![]() 平面DEFG,取DG的中点为M,连接AM、FM,证明
平面DEFG,取DG的中点为M,连接AM、FM,证明![]() ,推出
,推出![]() 平面ACGD.
平面ACGD.
![]() 以DG、DE、DA为方向建立空间直角坐标系,求出平面BGF法向量,通过点D到平面
以DG、DE、DA为方向建立空间直角坐标系,求出平面BGF法向量,通过点D到平面![]() 即平面
即平面![]() 的距离,求解即可.
的距离,求解即可.
(1)证明:已知如图:
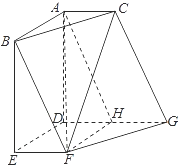
∵平面![]() 平面DEFG,平面
平面DEFG,平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴ADEB为平行四边形,![]() .
.
∴![]() 平面DEFG,
平面DEFG,
∵![]() 平面BEF,
平面BEF,
∴平面![]() 平面DEFG.
平面DEFG.
取DG的中点为M,连接AM、FM,
则由已知条件易证四边形DEFM是平行四边形,
∴![]() ,
,
又∵![]() ,
,
∴![]()
∴四边形ABFM是平行四边形,即![]() ,
,
又![]() 平面ACGD,
平面ACGD,
故![]() 平面ACGD.
平面ACGD.
(2)由(1)得![]() 平面
平面![]() ,所以
,所以![]() ,
,
根据几何关系得:![]()
以DG、DE、DA为方向建立空间直角坐标系,如图
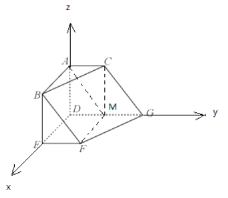
则![]() ,
,![]() ,
,![]()
所以![]() ,
,![]()
设平面![]() 法向量为
法向量为![]() ,
,
则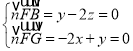 ,取
,取![]() 得
得![]()
所以点![]() 到平面
到平面![]() (即平面
(即平面![]() )的距离
)的距离
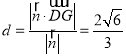 .
.

【题目】2019年9月1日,《西安市生活垃圾分类管理办法》正式实施.根据规定,生活垃圾分为可回收物、有害垃圾、厨余垃圾和其他垃圾,个人和单位如果不按规定进行垃圾分类将面临罚款,并纳入征信系统.为调查市民对垃圾分类的了解程度,某调查小组随机抽取了某小区的100位市民,请他们指出生活中若干项常见垃圾的种类,把能准确分类不少于3项的称为“比较了解”,少于三项的称为“不太了解”.调查结果如下:
0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 | |
男(人) | 1 | 5 | 15 | 8 | 6 | 7 | 3 |
女(人) | 0 | 4 | 11 | 13 | 10 | 12 | 5 |
(1)完成如下![]() 列联表并判断是否有99%的把握认为了解垃圾分类与性别有关?
列联表并判断是否有99%的把握认为了解垃圾分类与性别有关?
比较了解 | 不太了解 | 合计 | |
男 | |||
女 | |||
合计 |
(2)从对垃圾分类比较了解的市民中用分层抽样的方式抽取8位,现从这8位市民中随机选取两位,求至多有一位男市民的概率.
附: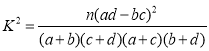
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |