题目内容
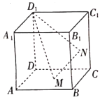
【题目】在正方体
中，如图，
分别是正方形
，
的中心.则下列结论正确的是（ ）
A.平面
与
的交点是的中点
B.平面与
的交点是的三点分点
C.平面与
的交点是的三等分点
D.平面将正方体分成两部分的体积比为1∶1
【答案】BC
【解析】
取
的中点
，延长
，
，并交于点
，连
并延长分别交
于
，连
并延长交
与
，平面四边形
为所求的截面，进而求出
在各边的位置，利用割补法求出多面体
的体积，即可求出结论.
如图，取的中点，延长，，并交于点，
连接并延长，设
，
，
连接
并延长交于点.连接
，
，
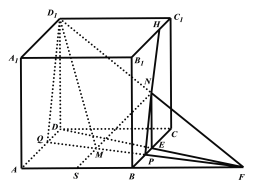
则平面四边形就是平面
与正方体的截面，如图所示.
，
为
的中位线，
为
中点，连
，
，
三点共线，取
中点
，连
，
则
，
，
为中点，
分别是正方形
的中心，
所以点
是线段靠近点
的三等分点，
点
是线段
靠近点
的三等分点，
点是线段靠近点
的三等分点.
做出线段的另一个三等分点
，
做出线段
靠近
的三等分点
，
连接
，
，
，
，
，
所以
从而平面将正方体分成两部分体积比为2∶1.
故选:BC.
练习册系列答案
口算题天天练系列答案
相关题目
