题目内容
设椭圆方程为 =1(a>b>0),短轴的一个顶点B与两焦点F1、F2组成的三角形的周长为4+2
=1(a>b>0),短轴的一个顶点B与两焦点F1、F2组成的三角形的周长为4+2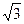 ,且∠F1BF2=
,且∠F1BF2= ,求椭圆方程.
,求椭圆方程.
 =1(a>b>0),短轴的一个顶点B与两焦点F1、F2组成的三角形的周长为4+2
=1(a>b>0),短轴的一个顶点B与两焦点F1、F2组成的三角形的周长为4+2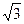 ,且∠F1BF2=
,且∠F1BF2= ,求椭圆方程.
,求椭圆方程.椭圆方程为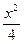 +y2=1
+y2=1
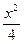 +y2=1
+y2=1由题意知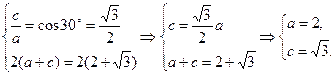
∴b2=a2-c2=1.
∴椭圆方程为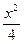 +y2=1.
+y2=1.
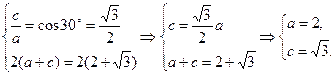
∴b2=a2-c2=1.
∴椭圆方程为
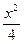 +y2=1.
+y2=1.
练习册系列答案
相关题目
题目内容
 =1(a>b>0),短轴的一个顶点B与两焦点F1、F2组成的三角形的周长为4+2
=1(a>b>0),短轴的一个顶点B与两焦点F1、F2组成的三角形的周长为4+2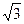 ,且∠F1BF2=
,且∠F1BF2= ,求椭圆方程.
,求椭圆方程.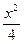 +y2=1
+y2=1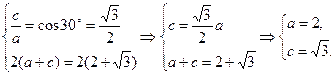
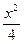 +y2=1.
+y2=1.