题目内容
设椭圆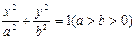 的焦点分别为
的焦点分别为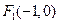 、
、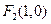 ,直线
,直线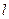 :
: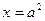 交
交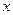 轴于点
轴于点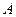 ,且
,且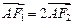 .
.
(1)试求椭圆的方程;
(2)过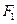 、
、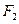 分别作互相垂直的两直线与椭圆分别交于
分别作互相垂直的两直线与椭圆分别交于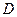 、
、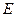 、
、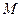 、
、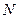 四点(如图所示),试求四边形
四点(如图所示),试求四边形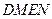 面积的最大值和最小值.
面积的最大值和最小值.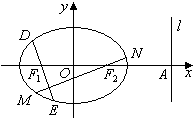
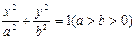 的焦点分别为
的焦点分别为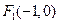 、
、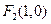 ,直线
,直线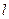 :
: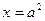 交
交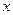 轴于点
轴于点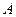 ,且
,且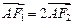 .
.(1)试求椭圆的方程;
(2)过
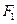 、
、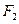 分别作互相垂直的两直线与椭圆分别交于
分别作互相垂直的两直线与椭圆分别交于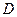 、
、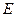 、
、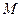 、
、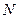 四点(如图所示),试求四边形
四点(如图所示),试求四边形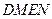 面积的最大值和最小值.
面积的最大值和最小值.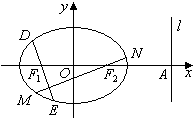
(1)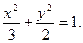
(2)最大值是4,最小值是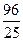
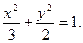
(2)最大值是4,最小值是
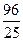
(1)由题意,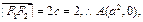
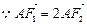
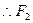 为
为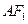 的中点
的中点
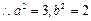
即:椭圆方程为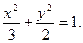 ……………(4分)
……………(4分)
(2)当直线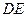 与
与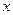 轴垂直时,
轴垂直时,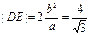 ,此时
,此时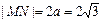 ,四边形
,四边形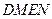 的面积
的面积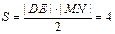 .同理当
.同理当 与
与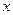 轴垂直时,也有四边形
轴垂直时,也有四边形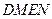 的面积
的面积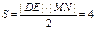 .…………………………………………6分
.…………………………………………6分
当直线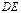 ,
,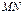 均与
均与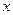 轴不垂直时,设
轴不垂直时,设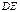 :
: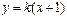 ,代入消去
,代入消去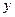 得:
得: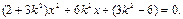 设
设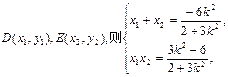
所以,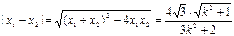 , 所以,
, 所以,
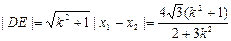 ,同理
,同理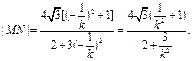
所以四边形的面积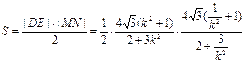
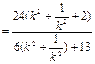 ………………………………10分
………………………………10分
令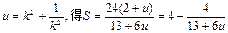 因为
因为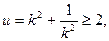 当
当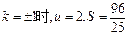 ,
,
且S是以u为自变量的增函数,所以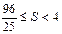 .
.
所以面积最大值是4.最小值是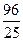 …………………………………………12分
…………………………………………12分
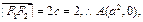
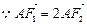
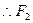 为
为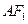 的中点
的中点 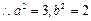
即:椭圆方程为
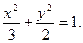 ……………(4分)
……………(4分)(2)当直线
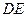 与
与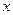 轴垂直时,
轴垂直时,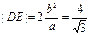 ,此时
,此时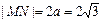 ,四边形
,四边形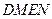 的面积
的面积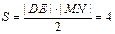 .同理当
.同理当 与
与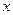 轴垂直时,也有四边形
轴垂直时,也有四边形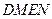 的面积
的面积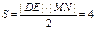 .…………………………………………6分
.…………………………………………6分当直线
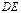 ,
,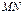 均与
均与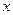 轴不垂直时,设
轴不垂直时,设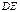 :
: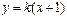 ,代入消去
,代入消去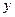 得:
得: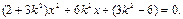 设
设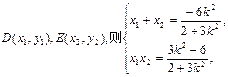
所以,
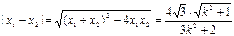 , 所以,
, 所以,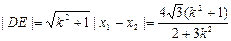 ,同理
,同理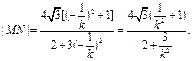
所以四边形的面积
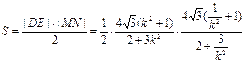
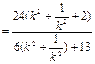 ………………………………10分
………………………………10分令
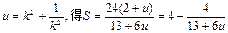 因为
因为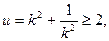 当
当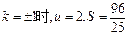 ,
,且S是以u为自变量的增函数,所以
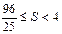 .
. 所以面积最大值是4.最小值是
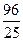 …………………………………………12分
…………………………………………12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
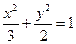 的左、右焦点分别为
的左、右焦点分别为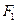 ,
,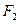 .过
.过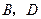 两点,过
两点,过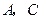 两点,且
两点,且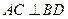 ,垂足为
,垂足为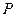 .
.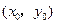 ,证明:
,证明: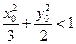 ;
;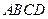 的面积的最小值.
的面积的最小值.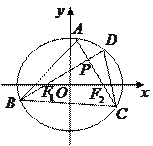
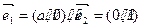 ,经过定点
,经过定点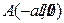 且方向向量为
且方向向量为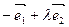 的直线与经过定点
的直线与经过定点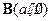 且方向向量为
且方向向量为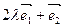 的直线交于点M,其中
的直线交于点M,其中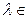 R,常数a>0.
R,常数a>0.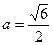 ,过点
,过点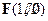 的直线与点M的轨迹交于C、D两点,求
的直线与点M的轨迹交于C、D两点,求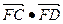 的取值范围.
的取值范围.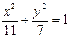 上一点到直线
上一点到直线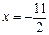 与到点(-2,0)的距离之比为
与到点(-2,0)的距离之比为 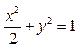 ,
, 经过点
经过点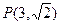 ,且与
,且与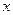 轴交于
轴交于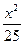 +
+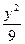 ="1"
="1"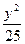 +
+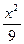 =1(y≠0)
=1(y≠0)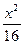 +
+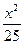 +
+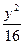 =1上一点,则
=1上一点,则 x+
x+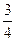 y的最小值为__________________.
y的最小值为__________________. =1(a>b>0),短轴的一个顶点B与两焦点F1、F2组成的三角形的周长为4+2
=1(a>b>0),短轴的一个顶点B与两焦点F1、F2组成的三角形的周长为4+2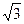 ,且∠F1BF2=
,且∠F1BF2= ,求椭圆方程.
,求椭圆方程.