题目内容
设椭圆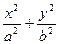 =1的焦点为F1、F2,P是椭圆上任意一点,一条斜率为
=1的焦点为F1、F2,P是椭圆上任意一点,一条斜率为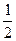 的直线交椭圆于A、B两点,如果当a变化时,总可同时满足:
的直线交椭圆于A、B两点,如果当a变化时,总可同时满足:
①∠F1PF2的最大值为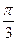 ;
;
②直线l:ax+y+1=0平分线段AB.
求a的取值范围.
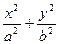 =1的焦点为F1、F2,P是椭圆上任意一点,一条斜率为
=1的焦点为F1、F2,P是椭圆上任意一点,一条斜率为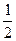 的直线交椭圆于A、B两点,如果当a变化时,总可同时满足:
的直线交椭圆于A、B两点,如果当a变化时,总可同时满足:①∠F1PF2的最大值为
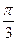 ;
;②直线l:ax+y+1=0平分线段AB.
求a的取值范围.
a>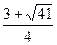 .
.
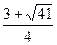 .
.由椭圆的定义及余弦定理得|F1F2|2=|PF1|2+|PF2|2-2|PF1||PF2|cos∠F1PF2=(|PF1|+|PF2|)2-
2|PF1|·|PF2|(1+cos∠F1PF2).
∴2|PF1||PF2|(1+cos∠F1PF2)=4a2-4c2=4b2.
∵|PF1||PF2|≤(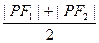 )2,
)2,
∴2(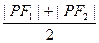 )2(1+cos∠F1PF2)≥4b2.
)2(1+cos∠F1PF2)≥4b2.
∴cos∠F1PF2≥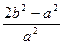 ,当且仅当|PF1|=|PF2|时取等号.由于∠F1PF2的最大值为
,当且仅当|PF1|=|PF2|时取等号.由于∠F1PF2的最大值为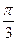 ,
,
∴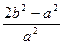 =
=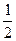 .
.
∴3a2=4b2,从而椭圆方程为3x2+4y2=3a2.
设AB的方程为y=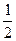 x+m,代入椭圆方程得4x2+4mx+4m2-3a2=0.
x+m,代入椭圆方程得4x2+4mx+4m2-3a2=0.
由Δ=16m2-4×4(4m2-3a2)>0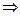 a2>m2.而AB的中点M(-
a2>m2.而AB的中点M(-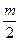 ,
,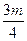 )在l上,
)在l上,
∴- +1=0,解得m=
+1=0,解得m=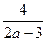 .
.
代入a2>m2,解得a>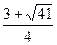 .
.
2|PF1|·|PF2|(1+cos∠F1PF2).
∴2|PF1||PF2|(1+cos∠F1PF2)=4a2-4c2=4b2.
∵|PF1||PF2|≤(
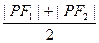 )2,
)2,∴2(
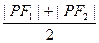 )2(1+cos∠F1PF2)≥4b2.
)2(1+cos∠F1PF2)≥4b2.∴cos∠F1PF2≥
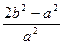 ,当且仅当|PF1|=|PF2|时取等号.由于∠F1PF2的最大值为
,当且仅当|PF1|=|PF2|时取等号.由于∠F1PF2的最大值为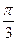 ,
,∴
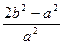 =
=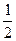 .
.∴3a2=4b2,从而椭圆方程为3x2+4y2=3a2.
设AB的方程为y=
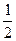 x+m,代入椭圆方程得4x2+4mx+4m2-3a2=0.
x+m,代入椭圆方程得4x2+4mx+4m2-3a2=0.由Δ=16m2-4×4(4m2-3a2)>0
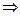 a2>m2.而AB的中点M(-
a2>m2.而AB的中点M(-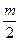 ,
,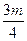 )在l上,
)在l上,∴-
 +1=0,解得m=
+1=0,解得m=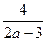 .
.代入a2>m2,解得a>
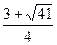 .
.
练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
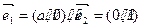 ,经过定点
,经过定点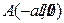 且方向向量为
且方向向量为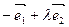 的直线与经过定点
的直线与经过定点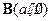 且方向向量为
且方向向量为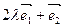 的直线交于点M,其中
的直线交于点M,其中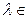 R,常数a>0.
R,常数a>0.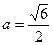 ,过点
,过点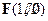 的直线与点M的轨迹交于C、D两点,求
的直线与点M的轨迹交于C、D两点,求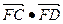 的取值范围.
的取值范围.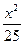 +
+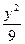 ="1"
="1"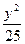 +
+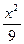 =1(y≠0)
=1(y≠0)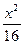 +
+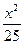 +
+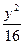 =1上一点,则
=1上一点,则 x+
x+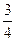 y的最小值为__________________.
y的最小值为__________________.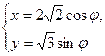 (φ为参数)上一点M与原点的连线与x轴正方向所成角为
(φ为参数)上一点M与原点的连线与x轴正方向所成角为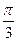 ,求点M的坐标.
,求点M的坐标.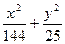 =1有两个公共点,则m的取值范围是( )
=1有两个公共点,则m的取值范围是( )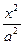 +
+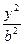 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=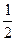 ,左焦点为F,A、B、C为其三个顶点,直线CF与AB交于D,则tan∠BDC的值等于( )
,左焦点为F,A、B、C为其三个顶点,直线CF与AB交于D,则tan∠BDC的值等于( )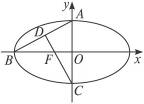
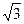 B.-3
B.-3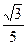 D.-
D.- =1(a>b>0),短轴的一个顶点B与两焦点F1、F2组成的三角形的周长为4+2
=1(a>b>0),短轴的一个顶点B与两焦点F1、F2组成的三角形的周长为4+2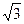 ,且∠F1BF2=
,且∠F1BF2= ,求椭圆方程.
,求椭圆方程.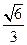 ,求椭圆的标准方程.
,求椭圆的标准方程.