题目内容
已知椭圆的中心在原点,焦点在坐标轴上,分别根据下列条件求椭圆的标准方程.
(1)长轴、短轴长之比为2∶1,一条准线为x+4=0;
(2)离心率为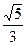
,一条准线为y=3.
(1)长轴、短轴长之比为2∶1,一条准线为x+4=0;
(2)离心率为
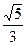,一条准线为y=3.1、椭圆方程为
=1.
2、椭圆方程为
=1.
=1.2、椭圆方程为
=1.(1)由题意得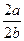
=2,即a="2b. " ①
∵x=-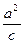
=-4,即a2="4c, " ②
又a2=b2+c2, ③
解①②③得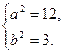
∴椭圆方程为=1.
(2)由题意得e=
=
, ⑤
y=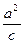="3. " ⑥
由⑤⑥得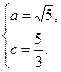
∴b2=a2-c2=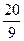
.
∴椭圆方程为=1.
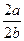=2,即a="2b. " ①∵x=-
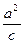=-4,即a2="4c, " ②又a2=b2+c2, ③
解①②③得
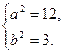
∴椭圆方程为
=1.(2)由题意得e=
=, ⑤y=
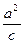="3. " ⑥由⑤⑥得
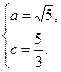
∴b2=a2-c2=
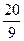.∴椭圆方程为
=1.
练习册系列答案
相关题目
，
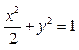(φ为参数)上一点M与原点的连线与x轴正方向所成角为
,求点M的坐标.
+
=1(a>b>0)的离心率e=
,左焦点为F,A、B、C为其三个顶点,直线CF与AB交于D,则tan∠BDC的值等于( )
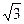B.-3
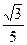D.-
+
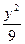=1上一点P到两焦点距离之积为m,则m最大时求P点坐标.
=1(a>b>0),短轴的一个顶点B与两焦点F1、F2组成的三角形的周长为4+2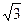
,且∠F1BF2=
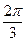,求椭圆方程.
+
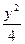=1的两个焦点,P是椭圆上一点,且|PF1|-|PF2|=1,则cos∠F1PF2=___________.
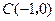及椭圆
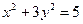，过点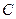
的动直线与椭圆相交于
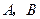两点.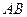
中点的横坐标是
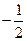，求直线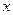
轴上是否存在点
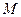，使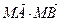
为常数？若存在，求出点