[题目]判断下列函数的奇偶性．(1)f(x)＝x2-|x|+1.x∈[-1,4], (2)f(x)＝,(3)f(x)＝, (4)f(x)＝题目和参考答案——青夏教育精英家教网—

题目内容

【题目】判断下列函数的奇偶性．

（1）f(x)＝x2－|x|＋1，x∈[－1,4]；（2）f(x)＝；

（3）f(x)＝；（4）f(x)＝

【答案】见解析

【解析】（1）虽然f(－x)＝f(x)，但定义域不关于原点对称，

故f(x)＝x2－|x|＋1，x∈[－1,4]是非奇非偶函数．

（2）由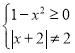得－1≤x<0，或0<x≤1.

故函数f(x)的定义域为[－1,0)∪(0,1]，关于原点对称，

且有x＋2>0.从而有f(x)＝＝＝，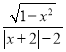

于是f(－x)＝－＝－f(x)．故函数f(x)为奇函数．

（3）∵≥0，∴－1≤x<1.

∴定义域不关于原点对称．∴f(x)为非奇非偶函数．

（4）当x>0时，x<0 ,f(－x)＝(－x)2＋(－x)＝x2－x；

当x<0时，x>0,f(－x)＝－(－x)2＋(－x)＝－x2－x.

∴f(－x)＝－f(x)，∴f(x)是奇函数．

练习册系列答案

相关题目

【题目】某制药厂生产某种颗粒状粉剂，由医药代表负责推销，若每包药品的生产成本为元，推销费用为元，预计当每包药品销售价为元时，一年的市场销售量为万包，若从民生考虑，每包药品的售价不得高于生产成本的，但为了鼓励药品研发，每包药品的售价又不得低于生产成本的

(1) 写出该药品一年的利润 (万元)与每包售价的函数关系式，并指出其定义域；

(2) 当每包药品售价为多少元时，年利润最大，最大值为多少？

【题目】每逢节假日，在微信好友群中发红包逐渐成为一种时尚，还能增进彼此的感情，2016年春节期间，小鲁在自己的微信好友群中，向在线的甲、乙、丙、丁四位好友随机发放红包，发放的规则为：每次发放一个，小鲁自己不抢，每个人抢到的概率相同．

（1）若小鲁随机发放了3个红包，求甲至少抢到一个红包的概率；

（2）若丁因有事暂时离线一段时间，而小鲁在这段时间内共发了3个红包，其中2个红包中各有10元，一个红包中有5元．设这段时间内乙所得红包的总钱数为元，求随机变量的分布列和数学期望．

【题目】设椭圆中心在坐标原点，A(2,0)，B(0,1)是它的两个顶点，直线y＝kx(k>0)与AB相交于点D，与椭圆相交于E、F两点．

(1)若＝6，求k的值；

(2)求四边形AEBF面积的最大值．

【题目】已知函数f(x)＝|2x－1|＋|x－2a|.

(1)当a＝1时，求f(x)≤3的解集；

(2)当x∈[1，2]时，f(x)≤3恒成立，求实数a的取值范围．

【题目】现从某班的一次期末考试中，随机的抽取了七位同学的数学(满分150分）、物理（满分110分）成绩如下表所示，数学、物理成绩分别用特征量表示，

特征量	1	2	3	4	5	6	7
t	101	124	119	106	122	118	115
y	74	83	87	75	85	87	83

求关于t的回归方程；

（2）利用（1）中的回归方程，分析数学成绩的变化对物理成绩的影响，并估计该班某学生数学成绩130分时，他的物理成绩(精确到个位).

附：回归方程中斜率和截距的最小二乘估计公式分别为：

．

【题目】已知幂函数(m∈Z)为偶函数，且在区间(0，＋∞)上是单调增函数．

（1）求函数f(x)的解析式；

（2）设函数，若g(x)>2对任意的x∈R恒成立，求实数c的取值范围．

【题目】本着健康、低碳的生活理念，租用公共自行车的人越来越多.租用公共自行车的收费标准是每车每次不超过两小时免费，超过两小时的部分每小时2元（不足1小时的部分按1小时计算）.甲乙两人相互独立租车（各租一车一次）.设甲、乙不超过两小时还车的概率分别为，；两小时以上且不超过三小时还车的概率分别为，；两人租车时间都不会超过四小时.