题目内容
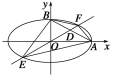
【题目】设椭圆中心在坐标原点,A(2,0),B(0,1)是它的两个顶点,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E、F两点.
(1)若![]() =6
=6![]() ,求k的值;
,求k的值;
(2)求四边形AEBF面积的最大值.
【答案】见解析
【解析】
解 (1)依题意得椭圆的方程为![]() +y2=1,直线AB,EF的方程分别为x+2y=2,y=kx(k>0).如图,设D(x0,kx0),E(x1,kx1),F(x2,kx2),其中x1<x2,且x1,x2满足方程(1+4k2)x2=4,故x2=-x1=
+y2=1,直线AB,EF的方程分别为x+2y=2,y=kx(k>0).如图,设D(x0,kx0),E(x1,kx1),F(x2,kx2),其中x1<x2,且x1,x2满足方程(1+4k2)x2=4,故x2=-x1=![]() .①
.①
由![]() =6
=6![]() 知x0-x1=6(x2-x0),
知x0-x1=6(x2-x0),
得x0=![]() (6x2+x1)=
(6x2+x1)=![]() x2=
x2=![]() ;
;
由D在AB上知x0+2kx0=2,
得x0=![]() .
.
所以![]() =
=![]() ,
,
化简得24k2-25k+6=0,
解得k=![]() 或k=
或k=![]() .
.
(2)根据点到直线的距离公式和①式知,点E,F到AB的距离分别为
h1=![]() =
=![]() ,
,
h2=![]() =
=![]() .
.
又|AB|=![]() =
=![]() ,
,
所以四边形AEBF的面积为
S=![]() |AB|(h1+h2)
|AB|(h1+h2)
=![]() ·
·![]() ·
·![]()
=![]()
=2![]() ≤2
≤2![]() ,
,
当4k2=1(k>0),即当k=![]() 时,上式取等号.
时,上式取等号.
所以S的最大值为2![]() .
.
即四边形AEBF面积的最大值为2![]() .
.

练习册系列答案
相关题目