题目内容
(本题满分14分)
如图,已知直三棱柱ABC—A1B1C1,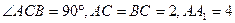 。E、F分别是棱CC1、AB中点。
。E、F分别是棱CC1、AB中点。
(1)求证: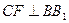 ;
;
(2)求四棱锥A—ECBB1的体积;
(3)判断直线CF和平面AEB1的位置关系,并加
以证明。
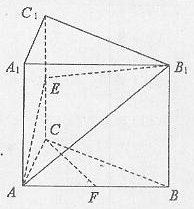
如图,已知直三棱柱ABC—A1B1C1,
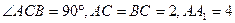 。E、F分别是棱CC1、AB中点。
。E、F分别是棱CC1、AB中点。(1)求证:
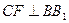 ;
;(2)求四棱锥A—ECBB1的体积;
(3)判断直线CF和平面AEB1的位置关系,并加
以证明。

(1)证明: 三棱柱ABC—A1B1C1是直棱柱,
三棱柱ABC—A1B1C1是直棱柱,
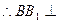 平面ABC 1分
平面ABC 1分
又 平面ABC, 2分
平面ABC, 2分
 3分
3分
(2)解: 三棱柱ABC—A1B1C1是直棱柱,
三棱柱ABC—A1B1C1是直棱柱,
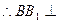 平面ABC,
平面ABC,
又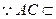 平面ABC
平面ABC




 平面ECBB1 6分
平面ECBB1 6分
 7分
7分
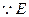 是棱CC1的中点,
是棱CC1的中点,

 8分
8分
 9分
9分
 (3)解:CF//平面AEB1,证明如下:
(3)解:CF//平面AEB1,证明如下:
取AB1的中点G,联结EG,FG
 分别是棱AB、AB1中点
分别是棱AB、AB1中点
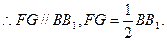
又

 四边形FGEC是平行四边形 11分
四边形FGEC是平行四边形 11分
 12分
12分
又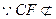 平面AEB,
平面AEB, 平面AEB1, 13分
平面AEB1, 13分
 平面AEB1。
平面AEB1。
 三棱柱ABC—A1B1C1是直棱柱,
三棱柱ABC—A1B1C1是直棱柱,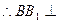 平面ABC 1分
平面ABC 1分又
 平面ABC, 2分
平面ABC, 2分 3分
3分(2)解:
 三棱柱ABC—A1B1C1是直棱柱,
三棱柱ABC—A1B1C1是直棱柱,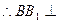 平面ABC,
平面ABC,又
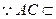 平面ABC
平面ABC



 平面ECBB1 6分
平面ECBB1 6分 7分
7分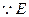 是棱CC1的中点,
是棱CC1的中点,
 8分
8分 9分
9分 (3)解:CF//平面AEB1,证明如下:
(3)解:CF//平面AEB1,证明如下:取AB1的中点G,联结EG,FG
 分别是棱AB、AB1中点
分别是棱AB、AB1中点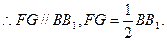
又


 四边形FGEC是平行四边形 11分
四边形FGEC是平行四边形 11分 12分
12分又
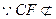 平面AEB,
平面AEB, 平面AEB1, 13分
平面AEB1, 13分 平面AEB1。
平面AEB1。略

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 (1) 求证:BD1∥平面C1DE;
(1) 求证:BD1∥平面C1DE;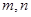 是不同的直线,
是不同的直线,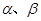 是不重合的平面,下列命题为真命题的是( )
是不重合的平面,下列命题为真命题的是( )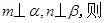
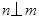
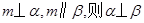
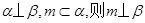

 90º,BC
90º,BC
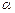 、
、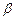 为两个确定的相交平面,a、b为一对异面直线,下列条件中能使a、b所成的角为定值的有 ( )
为两个确定的相交平面,a、b为一对异面直线,下列条件中能使a、b所成的角为定值的有 ( )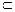
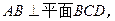 M、N分别是
M、N分别是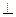 CD.
CD.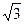 ,求直线AC与平面BCD所成的角.
,求直线AC与平面BCD所成的角.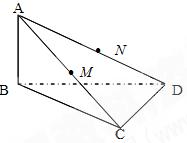
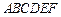 中,
中,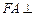 平面
平面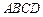 ,
,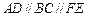 ,
,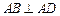 ,
,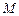 为
为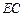 的中点,
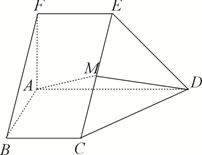
的中点,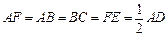 .
.
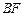 与
与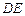 所成角的大小;
所成角的大小;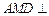 平面
平面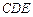 ;
;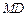 与平面
与平面