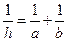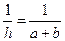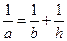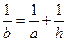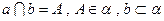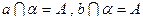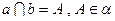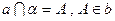题目内容
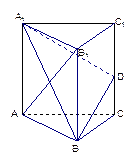
(本小题满分14分)如图,已知四棱锥P-ABCD中,PA⊥平面CDAB, ABCD是直角梯形,AD∥BC,∠BAD 90º,BC
90º,BC 2,PA
2,PA AB
AB 1.
1.

(1)求证:PD⊥AB;
(2)在线段PB上找一点E,使AE//平面PCD;
(3)求点D到平面PBC的距离.
 90º,BC
90º,BC 2,PA
2,PA AB
AB 1.
1.
(1)求证:PD⊥AB;
(2)在线段PB上找一点E,使AE//平面PCD;
(3)求点D到平面PBC的距离.
h=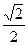
解:(1)∵PA⊥平面CDAB,AB 平面ABCD,∴PA⊥AB, …………2分
平面ABCD,∴PA⊥AB, …………2分
又AB⊥AD,PA AD=A,∴AB⊥平面PAD, …………3分
AD=A,∴AB⊥平面PAD, …………3分
∵PD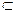 平面PAD,∴AB⊥PD. …………4分
平面PAD,∴AB⊥PD. …………4分
(2)取线段PB的中点E,PC的中点F,连结AE,EF,DF,
EF是△PBC中位线,∴EF∥BC,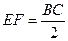 ; …………6分
; …………6分
又AD∥BC,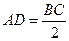 ,∴四边形EFDA是平行四边形, …………8分
,∴四边形EFDA是平行四边形, …………8分
∴AE∥DF,又AE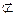 平面PDC,DF
平面PDC,DF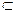 平面PDC,∴AE∥平面PDC,
平面PDC,∴AE∥平面PDC,
故线段PB的中点E是符合题意要求的点. …………10分
(3)设点D到平面PBC的距离为h.∵BC⊥AB,BC⊥PA,∴BC⊥平面PAB,∴BC⊥PB,
PB=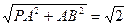 ,S△PBC=
,S△PBC=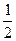 PB·BC=
PB·BC=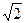 ,S△BDC=
,S△BDC=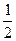 BC·AB="1 " …………12分
BC·AB="1 " …………12分
∵VP-BDC=VD-PBC,即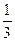 S△BDC·PA=
S△BDC·PA=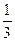 S△PBC·h,∴h=
S△PBC·h,∴h=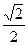 . …………14分
. …………14分
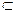 平面ABCD,∴PA⊥AB, …………2分
平面ABCD,∴PA⊥AB, …………2分又AB⊥AD,PA
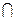 AD=A,∴AB⊥平面PAD, …………3分
AD=A,∴AB⊥平面PAD, …………3分∵PD
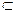 平面PAD,∴AB⊥PD. …………4分
平面PAD,∴AB⊥PD. …………4分(2)取线段PB的中点E,PC的中点F,连结AE,EF,DF,
EF是△PBC中位线,∴EF∥BC,
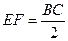 ; …………6分
; …………6分又AD∥BC,
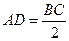 ,∴四边形EFDA是平行四边形, …………8分
,∴四边形EFDA是平行四边形, …………8分∴AE∥DF,又AE
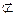 平面PDC,DF
平面PDC,DF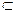 平面PDC,∴AE∥平面PDC,
平面PDC,∴AE∥平面PDC,故线段PB的中点E是符合题意要求的点. …………10分
(3)设点D到平面PBC的距离为h.∵BC⊥AB,BC⊥PA,∴BC⊥平面PAB,∴BC⊥PB,
PB=
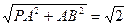 ,S△PBC=
,S△PBC=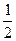 PB·BC=
PB·BC=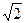 ,S△BDC=
,S△BDC=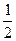 BC·AB="1 " …………12分
BC·AB="1 " …………12分∵VP-BDC=VD-PBC,即
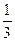 S△BDC·PA=
S△BDC·PA=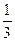 S△PBC·h,∴h=
S△PBC·h,∴h=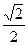 . …………14分
. …………14分
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 。E、F分别是棱CC1、AB中点。
。E、F分别是棱CC1、AB中点。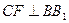 ;
;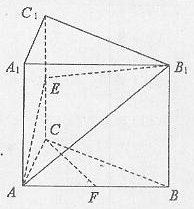
 的所有棱长都相等,且侧棱垂直于底面,由
的所有棱长都相等,且侧棱垂直于底面,由 沿棱柱侧面经过棱
沿棱柱侧面经过棱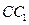 到点
到点 的最短路线长为
的最短路线长为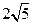 ,设这条最短路线与
,设这条最短路线与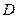 .
.
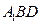 内是否存在过
内是否存在过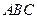 平行?证明你的判断;
平行?证明你的判断;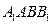 .
.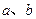 ,高为
,高为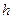 ,且侧面积等于两底面积之和,则下列关系正确的是
,且侧面积等于两底面积之和,则下列关系正确的是