题目内容
7.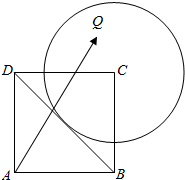 四边形ABCD是边长为1的正方形,以C为圆心的圆与直线BD相切,Q为圆内的任意一点,如图所示,$\overrightarrow{AQ}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,则y-x的取值范围是(-∞,$\frac{2-\sqrt{2}}{2}$]∪[$\frac{2+\sqrt{2}}{2}$,+∞).
四边形ABCD是边长为1的正方形,以C为圆心的圆与直线BD相切,Q为圆内的任意一点,如图所示,$\overrightarrow{AQ}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,则y-x的取值范围是(-∞,$\frac{2-\sqrt{2}}{2}$]∪[$\frac{2+\sqrt{2}}{2}$,+∞).
分析 以A为坐标原点建立如图所示直角坐标系,可得直线BD的方程x+y-1=0.算出以点C为圆心且与直线BD相切的圆方程为(x-1)2+(y-1)2=$\frac{1}{4}$.设Q(m,n),根据题中的向量等式算出P的坐标为(m,n),由Q在圆内或圆上得到(m-1)2+(n-1)2≤$\frac{1}{4}$.将此不等式化成关于m的一元二次不等式,利用根的判别式加以计算,可得y-x取值范围.
解答 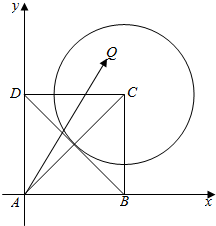 解:以A为坐标原点,AB、AD所在直线为x轴、y轴,建立平面直角坐标系如图所示:
解:以A为坐标原点,AB、AD所在直线为x轴、y轴,建立平面直角坐标系如图所示:
则A(0,0),D(0,1),C(1,1),B(1,0)
直线BD的方程为x+y=1,∴点C到BD的距离d=$\frac{\sqrt{2}}{2}$,
可得以点C为圆心,且与直线BD相切的圆方程为
(x-1)2+(y-1)2=$\frac{1}{2}$.
设Q(m,n),则$\overrightarrow{AQ}$=(m,n),$\overrightarrow{AD}$=(0,1),$\overrightarrow{AB}$=(1,0),
∵$\overrightarrow{AQ}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,(x,y∈R),
∴(m,n)=x(0,1)+y(1,0)=(x,y),
可得x=m且y=n,Q的坐标为(m,n).
∵Q在圆内或圆上,
∴(m-1)2+(n-1)2≤$\frac{1}{2}$,
设y-x=t,即n-m=t,得n=t+m,
代入上式化简整理得2m2-(4-2t)m-2t+$\frac{7}{4}$≤0,
若要上述不等式有实数解,
则△=(4-2t)2-4×2×($\frac{7}{4}$-2t)≥0,
化简得2t2-4t+1≥0,
解得t≥$\frac{2+\sqrt{2}}{2}$或t≤$\frac{2-\sqrt{2}}{2}$
∴y-x取值范围是(-∞,$\frac{2-\sqrt{2}}{2}$]∪[$\frac{2+\sqrt{2}}{2}$,+∞).
故答案为:(-∞,$\frac{2-\sqrt{2}}{2}$]∪[$\frac{2+\sqrt{2}}{2}$,+∞).
点评 本题在直角梯形中给出满足条件的向量式,求参数的取值范围.着重考查了直线的方程、点到直线的距离公式、圆的标准方程、直线与圆的位置关系与向量的坐标运算等知识,属于中档题.同时考查了逻辑推理能力与计算能力,考查了数形结合、转化化归的数学思想,是一道不错的综合题.

 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案| A. | (-∞,-1)∪(0,+∞) | B. | (-∞,-1)∪(0,1)∪(1,+∞) | C. | (-1,0)∪(1,+∞) | D. | (-1,0)∪(0,1) |
| A. | $\frac{1}{6}$ | B. | $\frac{5}{12}$ | C. | $\frac{7}{12}$ | D. | $\frac{1}{3}$ |
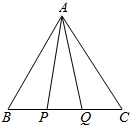 如图,在边长为6的正三角形△ABC内,△APQ的边PQ在BC边上滑动且PQ=2,求△APQ三边的平方和的最大值与最小值.
如图,在边长为6的正三角形△ABC内,△APQ的边PQ在BC边上滑动且PQ=2,求△APQ三边的平方和的最大值与最小值.