题目内容
17.求下列函数定积分.(1)已知f(x)=4x3+4sinx,求${∫}_{-\frac{π}{2}}^{\frac{π}{2}}$f(x)dx;
(2)已知f(x)=$\left\{\begin{array}{l}{{x}^{2},(x≤0)}\\{cosx-1,(x>0)}\end{array}\right.$,求${∫}_{-1}^{1}$f(x)dx.
分析 (1)由和的积分等于积分的和展开,然后求出被积函数的原函数,直接由微积分基本定理得答案;
(2)把积分区间分段,然后求出被积函数的原函数,再由微积分基本定理得答案.
解答 解:(1)由于f(x)=4x3+4sinx,
则${∫}_{-\frac{π}{2}}^{\frac{π}{2}}$f(x)dx=${∫}_{-\frac{π}{2}}^{\frac{π}{2}}$(4x3+4sinx)dx
=${∫}_{-\frac{π}{2}}^{\frac{π}{2}}$4x3dx+${∫}_{-\frac{π}{2}}^{\frac{π}{2}}$4sinxdx
=(x4)${|}_{-\frac{π}{2}}^{\frac{π}{2}}$+(-4cosx)${|}_{-\frac{π}{2}}^{\frac{π}{2}}$
=$(\frac{π}{2})^{4}-(-\frac{π}{2})^{4}$+$(-4cos\frac{π}{2})-(-4cos(-\frac{π}{2}))$
=0;
(2)由于f(x)=$\left\{\begin{array}{l}{{x}^{2},(x≤0)}\\{cosx-1,(x>0)}\end{array}\right.$,
则${∫}_{-1}^{1}$f(x)dx=${∫}_{-1}^{0}$x2dx+${∫}_{0}^{1}$(cosx-1)dx
=$(\frac{1}{3}{x}^{3}){|}_{-1}^{0}$+$(sinx-x){|}_{0}^{1}$
=0+$\frac{1}{3}$+sin1-1-0
=sin1-$\frac{2}{3}$.
点评 本题考查了定积分的计算,考查了微积分基本定理,关键是求出原函数,属于基础题.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案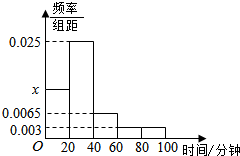 古人是说的好:书中自有黄金屋,书中自有颜如玉,课外阅读对大学生来讲是一种最有效的自主学习方式,某大学对本校大一学生进行了课外阅读现状的调查,从调查中发现大一学生平均每天课外阅读时间的范围是[0,100](单位:分钟),求所得的平均每天课外阅读时间的数据绘制成平率分布直方图(如图),样本数据分组为[0,20),[20,40),[60,80),[80,100].
古人是说的好:书中自有黄金屋,书中自有颜如玉,课外阅读对大学生来讲是一种最有效的自主学习方式,某大学对本校大一学生进行了课外阅读现状的调查,从调查中发现大一学生平均每天课外阅读时间的范围是[0,100](单位:分钟),求所得的平均每天课外阅读时间的数据绘制成平率分布直方图(如图),样本数据分组为[0,20),[20,40),[60,80),[80,100].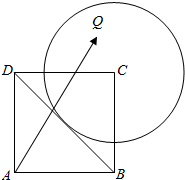 四边形ABCD是边长为1的正方形,以C为圆心的圆与直线BD相切,Q为圆内的任意一点,如图所示,$\overrightarrow{AQ}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,则y-x的取值范围是(-∞,$\frac{2-\sqrt{2}}{2}$]∪[$\frac{2+\sqrt{2}}{2}$,+∞).
四边形ABCD是边长为1的正方形,以C为圆心的圆与直线BD相切,Q为圆内的任意一点,如图所示,$\overrightarrow{AQ}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,则y-x的取值范围是(-∞,$\frac{2-\sqrt{2}}{2}$]∪[$\frac{2+\sqrt{2}}{2}$,+∞).