题目内容
2.已知函数f(x)=$\frac{{ax}^{2}+bx}{x+2}$,函数y=f(x)在点(2,f(2))处的切线方程是5x-4y+2=0.(1)求a,b的值;
(2)设g(x)=ln(x+2)-mf(x)-ln2,若当x∈[0,+∞)时,恒有g(x)≤0,求m的取值范围.
分析 (1)求导函数,利用曲线y=f(x)在点(2,f(2))处的切线方程是5x-4y+2=0,建立方程组,即可求a,b的值;
(2)由(1)知:f(x)=$\frac{{x}^{2}+4x}{x+2}$,g(x)=ln(x+2)-m$\frac{{x}^{2}+4x}{x+2}$-ln2(x>-1),求导函数,构建新函数h(x)=-mx2+(1-4m)x+2-8m,分类讨论,确定g(x)在[0,+∞)上的单调性,即可得到结论.
解答 解:(1)求导函数,可得f′(x)=$\frac{(2ax+b)(x+2)-(a{x}^{2}+bx)}{(x+2)^{2}}$=$\frac{a{x}^{2}+4ax+2b}{(x+2)^{2}}$.
∵曲线y=f(x)在点(2,f(2))处的切线方程是5x-4y+2=0.
∴$\left\{\begin{array}{l}{f(2)=3}\\{f′(2)=\frac{5}{4}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{\frac{2a+b}{2}=3}\\{\frac{6a+b}{8}=\frac{5}{4}}\end{array}\right.$,解得:a=1,b=4;
(2)由(1)知:f(x)=$\frac{{x}^{2}+4x}{x+2}$,
∴g(x)=ln(x+2)-m$\frac{{x}^{2}+4x}{x+2}$-ln2(x>-1),
则g′(x)=$\frac{-m{x}^{2}+(1-4m)x+2-8m}{(x+2)^{2}}$,
令h(x)=-mx2+(1-4m)x+2-8m,
当m=0时,h(x)=x+2,在x∈[0,+∞)时,h(x)>0,∴g′(x)>0,即g(x)在[0,+∞)上是增函数,则g(x)≥g(0)=0,不满足题设;
当m<0时,∵-$\frac{1-4m}{-2m}$=$\frac{1}{2m}-2<0$且h(0)=2-8m>0,
∴x∈[0,+∞)时,h(x)>0,g′(x)>0,即g(x)在[0,+∞)上是增函数,则g(x)≥g(0)=0,不满足题设;
当0<m<$\frac{1}{4}$时,则△=(1-4m)2+4m(2-8m)=1-16m2>0,
由h(x)=0得,${x}_{1}=\frac{4m-1-\sqrt{1-16{m}^{2}}}{-2m}$>0,${x}_{2}=\frac{4m-1+\sqrt{1-16{m}^{2}}}{-2m}$<0.
则x∈[0,x1)时,h(x)>0,g′(x)>0即g(x)在[0,x1)上是增函数,则g(x2)≥g(0)=0,不满足题设;
当m≥$\frac{1}{4}$时,△=(1-4m)2+4m(2-8m)=1-16m2≤0,h(x)≤0,g′(x)≤0,即g(x)在[0,+∞)上是减函数,则g(x)≤g(0)=0,满足题设.
综上所述,m∈[$\frac{1}{4}$,+∞).
点评 本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性,考查分类讨论的数学思想,正确求导,合理分类是关键,是压轴题.

| A. | 若m⊥n,n?α,则m⊥α | B. | 若m∥α,n∥α,则m∥n | C. | 若m⊥α,n∥m,则n⊥α | D. | 若α⊥γ,β⊥γ,则α∥β |
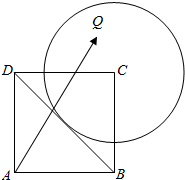 四边形ABCD是边长为1的正方形,以C为圆心的圆与直线BD相切,Q为圆内的任意一点,如图所示,$\overrightarrow{AQ}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,则y-x的取值范围是(-∞,$\frac{2-\sqrt{2}}{2}$]∪[$\frac{2+\sqrt{2}}{2}$,+∞).
四边形ABCD是边长为1的正方形,以C为圆心的圆与直线BD相切,Q为圆内的任意一点,如图所示,$\overrightarrow{AQ}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,则y-x的取值范围是(-∞,$\frac{2-\sqrt{2}}{2}$]∪[$\frac{2+\sqrt{2}}{2}$,+∞).