题目内容
18.已知f(x)=$\frac{2x}{{x}^{2}+4}$.(1)若关于x的不等式f(x)>k的解集是{x|x<-4,或x>-1},求实数k的值;
(2)设g(x)=x2-2mx+3,x∈[1,3],若对任意的x1>0,总存在x2∈[1,3]使得f(x1)<g(x2)成立,求实数m的取值范围.
分析 (1)由x2+4>0,把f(x)>k化为2x>k(x2+4),利用一元二次不等式的解集求出k的值;
(2)根据题意,把问题转化为f(x)max<g(x)max,求出对应区间上的最大值,列出不等式,
即可求出m的取值范围.
解答 解:(1)∵x2+4>0,
∴不等式f(x)>k可化为2x>k(x2+4),
即kx2-2x+4k<0;
又该不等式的解集是{x|x<-4,或x>-1},
∴$\left\{\begin{array}{l}{k<0}\\{-4-1=\frac{2}{k}}\end{array}\right.$,
解得k=-$\frac{2}{5}$;
(2)对任意x1>0,总存在x2∈[1,3],使得f(x1)<g(x2)成立,
等价于f(x)max<g(x)max;
而f(x)在x>0时的最大值为f(2)=$\frac{1}{2}$,
且g(x)=x2-2mx+3,x∈[1,3],
∴m<2时,g(x)在[1,3]上的最大值是g(3)=12-m,
令12-m>$\frac{1}{2}$,解得m<$\frac{23}{2}$,
∴应取m<2;
m≥2时,g(x)在[1,3]上的最大值是g(1)=4-2m,
令4-2m>$\frac{1}{2}$,解得m<$\frac{7}{4}$;
不合题意,舍去;
综上,实数m的取值范围是{m|m<2}.
点评 本题考查了一元二次不等式的解法与应用问题,也考查了转化思想的应用问题,考查了分类讨论思想的应用问题,是综合性题目.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
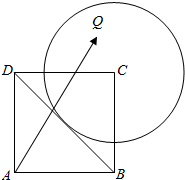 四边形ABCD是边长为1的正方形,以C为圆心的圆与直线BD相切,Q为圆内的任意一点,如图所示,$\overrightarrow{AQ}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,则y-x的取值范围是(-∞,$\frac{2-\sqrt{2}}{2}$]∪[$\frac{2+\sqrt{2}}{2}$,+∞).
四边形ABCD是边长为1的正方形,以C为圆心的圆与直线BD相切,Q为圆内的任意一点,如图所示,$\overrightarrow{AQ}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,则y-x的取值范围是(-∞,$\frac{2-\sqrt{2}}{2}$]∪[$\frac{2+\sqrt{2}}{2}$,+∞).