题目内容
17.椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点分别为F1,F2,斜率为k的直线l过右焦点F2,且与椭圆交于A,B两点,与y轴交于M点,若$\overrightarrow{MB}=2\overrightarrow{B{F}_{2}}$.当|k|≤2$\sqrt{6}$时,则椭圆的离心率的取值范围是[$\sqrt{\frac{29-5\sqrt{31}}{2}}$,1).分析 设椭圆离心率为e,设F2的坐标为(c,0),设l的方程为y=kx+m,则可求得l与y轴的交点,进而求得B点坐标,带椭圆方程求得e和k的关系式,进而根据k的范围得出关于e的不等式,求得e的范围.
解答 解:设椭圆离心率为e,设F2的坐标为(c,0),其中c2=a2-b2,
设l的方程为y=kx+m,则l与y轴的交点为(0,m),m=-kc,
所以B点的坐标为($\frac{c}{2}$,-$\frac{kc}{2}$),将B点坐标代入椭圆方程化简e2+$\frac{{k}^{2}}{\frac{1}{{e}^{2}}-1}$=4,
所以k2=(4-e2)•($\frac{1}{{e}^{2}}$-1)≤24,即e4-29e2+4≤0,解之可得,$\frac{29-5\sqrt{31}}{2}$≤e2≤$\frac{29+5\sqrt{31}}{2}$,
又有椭圆的性质,所以$\sqrt{\frac{29-5\sqrt{31}}{2}}$≤e<1,
因此椭圆C的离心率取值范围为[$\sqrt{\frac{29-5\sqrt{31}}{2}}$,1).
故答案为:[$\sqrt{\frac{29-5\sqrt{31}}{2}}$,1).
点评 本题主要考查了椭圆的简单性质.解题的关键是充分挖掘题目的隐含条件,寻找量与量间的关系灵活转化.

练习册系列答案
相关题目
5.椭圆$\frac{x^2}{4}$+$\frac{y^2}{9}$=1与曲线$\frac{x^2}{9-k}$+$\frac{{y{\;}^2}}{4-k}$=1(0<k<4)的关系是( )
| A. | 有相等的焦距,又有相同的焦点 | B. | 有相等的焦距,但是不同的焦点 | ||
| C. | 有不相等的焦距,又是不同的焦点 | D. | 有不相等的焦距,但有相同的焦点 |
12.设m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列命题正确的是( )
| A. | 若m⊥n,n?α,则m⊥α | B. | 若m∥α,n∥α,则m∥n | C. | 若m⊥α,n∥m,则n⊥α | D. | 若α⊥γ,β⊥γ,则α∥β |
2.在区间[1,3]上任取一个实数x,则1.5≤x≤2的概率等于( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
6.已知函数f(x)=$\left\{\begin{array}{l}{(5-a)x+a-6,x≤4}\\{2{a}^{x-3},x>4}\end{array}\right.$,数列{an}满足an=f(n)(n∈N+),且数列{an}是单调递增数列,则实数a的取值范围是( )
| A. | (1,5) | B. | (2,5) | C. | ($\frac{14}{5}$,5) | D. | [$\frac{14}{5}$,5) |
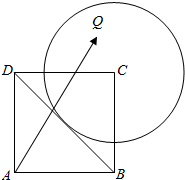 四边形ABCD是边长为1的正方形,以C为圆心的圆与直线BD相切,Q为圆内的任意一点,如图所示,$\overrightarrow{AQ}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,则y-x的取值范围是(-∞,$\frac{2-\sqrt{2}}{2}$]∪[$\frac{2+\sqrt{2}}{2}$,+∞).
四边形ABCD是边长为1的正方形,以C为圆心的圆与直线BD相切,Q为圆内的任意一点,如图所示,$\overrightarrow{AQ}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,则y-x的取值范围是(-∞,$\frac{2-\sqrt{2}}{2}$]∪[$\frac{2+\sqrt{2}}{2}$,+∞).