题目内容
15.已知函数f(x)=2lnx-x2(1)求函数y=f(x)在[$\frac{1}{2}$,2]上的最大值;
(2)函数h(x)=f(x)-mx的图象与x轴交于两点A(x1,0),B(x2,0)且0<x1<x2,又y=h′(x)是y=h(x)的导函数,若正常函数α,β满足条件α+β=1,β≥α,证明:h′(αx1+βx2)<0.
分析 (1)求导,利用导数求极致的方法求闭区间的最值
(2)把交点代人,求出m的关系;求h′(αx1+βx2),利用构造函数的方法,证明问题.
解答 解:f′(x)=$\frac{2}{x}$-2x=$\frac{2(1+x)(1-x)}{x}$,
在[$\frac{1}{2}$,1)上,f′(x)>0,f(x)递增,
在[1,2)上,f′(x)≤0,f(x)递减,
∴求函数y=f(x)在[$\frac{1}{2}$,2]上的最大值为f(1)=-1;
(2)h(x)=f(x)-mx=2lnx-x2-mx,
h′(x)=$\frac{2}{x}$-2x-m,
∵h(x1)=0,h(x2)=0,
∴2lnx1-x12-mx1=0 ①
2lnx2-x22-mx2=0 ②
①-②得m=$\frac{2ln\frac{{x}_{1}}{{x}_{2}}}{{x}_{1}-{x}_{2}}$-(x1+x2),
h′(αx1+βx2)=$\frac{2}{α{x}_{1}+β{x}_{2}}$-2(αx1+βx2)-m,
α+β=1,β≥α知β=1-α,$α≤\frac{1}{2}$,
h′(αx1+βx2)=$\frac{2}{α({x}_{1}-{x}_{2})+{x}_{2}}$-$\frac{2ln\frac{{x}_{1}}{{x}_{2}}}{{x}_{1}{-x}_{2}}$+(1-2α)(x1-x2)
∵$α≤\frac{1}{2}$,
∴(1-2α)(x1-x2)<0
只需证$\frac{2}{α({x}_{1}-{x}_{2})+{x}_{2}}$<$\frac{2ln\frac{{x}_{1}}{{x}_{2}}}{{x}_{1}{-x}_{2}}$
即证$\frac{α({x}_{1}-{x}_{2})+{x}_{2}}{{x}_{1}-{x}_{2}}ln\frac{{x}_{1}}{{x}_{2}}$>1
即(αx1+βx2)ln$\frac{{x}_{1}}{{x}_{2}}$<x1-x2,同时除以x2得
(α$\frac{{x}_{1}}{{x}_{2}}$+β)ln$\frac{{x}_{1}}{{x}_{2}}$<$\frac{{x}_{1}}{{x}_{2}}$-1
令t=$\frac{{x}_{1}}{{x}_{2}}$
∴只需证(αt+β)lnt-t+1<0
令r(t)=(αt+β)lnt-t+1 0<t<1
r′(t)=αlnt+α+$\frac{β}{t}$-1
r″(t)=$\frac{αt-β}{{t}^{2}}$<0,r′(t)递减
∴r′(t)>r′(1)=α+β-1=0
∴r(t)递增
r(t)<r(1)=0
∴(αt+β)lnt-t+1<0
∴h′(αx1+βx2)<0.
点评 考察了导函数的应用和利用构造函数的方法,结合导数求不等式.难度较大.

 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案| A. | 有相等的焦距,又有相同的焦点 | B. | 有相等的焦距,但是不同的焦点 | ||
| C. | 有不相等的焦距,又是不同的焦点 | D. | 有不相等的焦距,但有相同的焦点 |
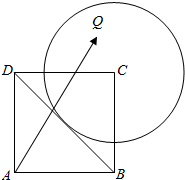 四边形ABCD是边长为1的正方形,以C为圆心的圆与直线BD相切,Q为圆内的任意一点,如图所示,$\overrightarrow{AQ}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,则y-x的取值范围是(-∞,$\frac{2-\sqrt{2}}{2}$]∪[$\frac{2+\sqrt{2}}{2}$,+∞).
四边形ABCD是边长为1的正方形,以C为圆心的圆与直线BD相切,Q为圆内的任意一点,如图所示,$\overrightarrow{AQ}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,则y-x的取值范围是(-∞,$\frac{2-\sqrt{2}}{2}$]∪[$\frac{2+\sqrt{2}}{2}$,+∞).