题目内容
16.甲、乙两人各抛掷一次正方体骰子(六个面分别标有数字1,2,3,4,5,6),设甲、乙所抛掷骰子朝上的面的点数分别为x,y,则满足x>y的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{5}{12}$ | C. | $\frac{7}{12}$ | D. | $\frac{1}{3}$ |
分析 本题是一个古典概型,试验发生所包含的事件是甲、乙两人各抛掷一次正方体骰子点数分别为x、y得到36种不同情况,统计满足x>y的个数,代入古典概型概率计算公式,可得答案.
解答 解:由题意知本题是一个古典概型,
∵试验发生所包含的事件是甲、乙两人各抛掷一次正方体骰子点数分别为x、y得到不同的事件数是36,
满足条件的事件x>y有,
当x是2时,y是1;
当x是3时,y是1,2;
当x是4时,y是1,2,3;
当x是5时,y是1,2,3,4;
当x是6时,y是1,2,3,4,5;
共有15种结果,
∴x>y的概率是:$\frac{15}{36}$=$\frac{5}{12}$,
故选B.
点评 本题考查了古典概型的概率计算公式,难度不大,是基础题目.

练习册系列答案
相关题目
5.椭圆$\frac{x^2}{4}$+$\frac{y^2}{9}$=1与曲线$\frac{x^2}{9-k}$+$\frac{{y{\;}^2}}{4-k}$=1(0<k<4)的关系是( )
| A. | 有相等的焦距,又有相同的焦点 | B. | 有相等的焦距,但是不同的焦点 | ||
| C. | 有不相等的焦距,又是不同的焦点 | D. | 有不相等的焦距,但有相同的焦点 |
6.已知函数f(x)=$\left\{\begin{array}{l}{(5-a)x+a-6,x≤4}\\{2{a}^{x-3},x>4}\end{array}\right.$,数列{an}满足an=f(n)(n∈N+),且数列{an}是单调递增数列,则实数a的取值范围是( )
| A. | (1,5) | B. | (2,5) | C. | ($\frac{14}{5}$,5) | D. | [$\frac{14}{5}$,5) |
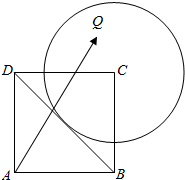 四边形ABCD是边长为1的正方形,以C为圆心的圆与直线BD相切,Q为圆内的任意一点,如图所示,$\overrightarrow{AQ}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,则y-x的取值范围是(-∞,$\frac{2-\sqrt{2}}{2}$]∪[$\frac{2+\sqrt{2}}{2}$,+∞).
四边形ABCD是边长为1的正方形,以C为圆心的圆与直线BD相切,Q为圆内的任意一点,如图所示,$\overrightarrow{AQ}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,则y-x的取值范围是(-∞,$\frac{2-\sqrt{2}}{2}$]∪[$\frac{2+\sqrt{2}}{2}$,+∞).