ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌвбжЊЭждВC1гыC2ЕФжааФдкзјБъдЕуOЃЌГЄжсОљЮЊMNЧвдкxжсЩЯЃЌЖЬжсГЄЗжБ№ЮЊ2mЃЌ2nЃЈmЃОnЃЉЃЌЙ§дЕуЧвВЛгыxжсжиКЯЕФжБЯпlгыC1 ЃЌ C2ЕФЫФИіНЛЕуАДзнзјБъДгДѓЕНаЁвРДЮЮЊAЃЌBЃЌCЃЌDЃЌМЧ ![]() ЃЌЁїBDMКЭЁїABNЕФУцЛ§ЗжБ№ЮЊS1КЭS2 ЃЎ
ЃЌЁїBDMКЭЁїABNЕФУцЛ§ЗжБ№ЮЊS1КЭS2 ЃЎ 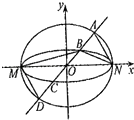
ЃЈ1ЃЉЕБжБЯпlгыyжсжиКЯЪБЃЌШєS1=ІЫS2 ЃЌ ЧѓІЫЕФжЕЃЛ
ЃЈ2ЃЉЕБІЫБфЛЏЪБЃЌЪЧЗёДцдкгызјБъжсВЛжиКЯЕФжБЯпlЃЌЪЙЕУS1=ІЫS2ЃПВЂЫЕУїРэгЩЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКвдЬтвтПЩЩшЭждВC1КЭC2ЕФЗНГЬЗжБ№ЮЊ
![]() ЃЌ
ЃЌ ![]() ЃЎЦфжаaЃОmЃОnЃО0ЃЌ
ЃЎЦфжаaЃОmЃОnЃО0ЃЌ
![]() ЃО1ЃЎ
ЃО1ЃЎ
ШчЭМ1ЃЌШєжБЯпlгыyжсжиКЯЃЌМДжБЯпlЕФЗНГЬЮЊx=0ЃЌдђ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
Ыљвд ![]() ЃЎ
ЃЎ
дкC1КЭC2ЕФЗНГЬжаЗжБ№Сюx=0ЃЌПЩЕУyA=mЃЌyB=nЃЌyD=ЉmЃЌ
гкЪЧ ![]() ЃЎ
ЃЎ
Шє ![]() ЃЌдђ
ЃЌдђ ![]() ЃЌЛЏМђЕУІЫ2Љ2ІЫЉ1=0ЃЌгЩІЫЃО1ЃЌНтЕУ
ЃЌЛЏМђЕУІЫ2Љ2ІЫЉ1=0ЃЌгЩІЫЃО1ЃЌНтЕУ ![]() ЃЎ
ЃЎ
ЙЪЕБжБЯпlгыyжсжиКЯЪБЃЌШєS1=ІЫS2ЃЌдђ ![]() ЃЎ
ЃЎ
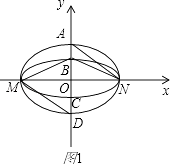
ЃЈ2ЃЉНтЃКШчЭМ2ЃЌШєДцдкгызјБъжсВЛжиКЯЕФжБЯпlЃЌЪЙЕУS1=ІЫS2ЃЌИљОнЖдГЦадЃЌ
ВЛЗСЩшжБЯпlЃКy=kxЃЈkЃО0ЃЉЃЌ
ЕуMЃЈЉaЃЌ0ЃЉЃЌNЃЈaЃЌ0ЃЉЕНжБЯпlЕФОрРыЗжБ№ЮЊd1ЃЌd2ЃЌдђ
![]() ЃЌЫљвдd1=d2ЃЎ
ЃЌЫљвдd1=d2ЃЎ
гж ![]() ЃЌЫљвд
ЃЌЫљвд ![]() ЃЌМД|BD|=ІЫ|AB|ЃЎ
ЃЌМД|BD|=ІЫ|AB|ЃЎ
гЩЖдГЦадПЩжЊ|AB|=|CD|ЃЌЫљвд|BC|=|BD|Љ|AB|=ЃЈІЫЉ1ЃЉ|AB|ЃЌ
|AD|=|BD|+|AB|=ЃЈІЫ+1ЃЉ|AB|ЃЌгкЪЧ ![]() ЃЎ
ЃЎ
НЋlЕФЗНГЬЗжБ№гыC1КЭC2ЕФЗНГЬСЊСЂЃЌПЩЧѓЕУ
![]()
ИљОнЖдГЦадПЩжЊxC=ЉxBЃЌxD=ЉxAЃЌгкЪЧ
![]() Ђк
Ђк
ДгЖјгЩЂйКЭЂкПЩЕУ
![]() Ђл
Ђл
Сю ![]() ЃЌдђгЩmЃОnЃЌПЩЕУtЁй1ЃЌгкЪЧгЩЂлПЩЕУ
ЃЌдђгЩmЃОnЃЌПЩЕУtЁй1ЃЌгкЪЧгЩЂлПЩЕУ ![]() ЃЎ
ЃЎ
вђЮЊkЁй0ЃЌЫљвдk2ЃО0ЃЎгкЪЧЂлЙигкkгаНтЃЌЕБЧвНіЕБ ![]() ЃЌ
ЃЌ
ЕШМлгк ![]() ЃЌгЩІЫЃО1ЃЌНтЕУ
ЃЌгЩІЫЃО1ЃЌНтЕУ ![]() ЃЌ
ЃЌ
МД ![]() ЃЌгЩІЫЃО1ЃЌНтЕУ
ЃЌгЩІЫЃО1ЃЌНтЕУ ![]() ЃЌЫљвд
ЃЌЫљвд
ЕБ ![]() ЪБЃЌВЛДцдкгызјБъжсВЛжиКЯЕФжБЯпlЃЌЪЙЕУS1=ІЫS2ЃЛ
ЪБЃЌВЛДцдкгызјБъжсВЛжиКЯЕФжБЯпlЃЌЪЙЕУS1=ІЫS2ЃЛ
ЕБ ![]() ЪБЃЌДцдкгызјБъжсВЛжиКЯЕФжБЯпlЃЌЪЙЕУS1=ІЫS2ЃЎ
ЪБЃЌДцдкгызјБъжсВЛжиКЯЕФжБЯпlЃЌЪЙЕУS1=ІЫS2ЃЎ
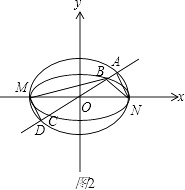
ЁОНтЮіЁПЃЈ1ЃЉЩшГіСНИіЭждВЕФЗНГЬЃЌЕБжБЯпlгыyжсжиКЯЪБЃЌЧѓГіЁїBDMКЭЁїABNЕФУцЛ§S1КЭS2 ЃЌ жБНггЩУцЛ§БШ=ІЫСаЪНЧѓІЫЕФжЕЃЛЃЈ2ЃЉМйЩшДцдкгызјБъжсВЛжиКЯЕФжБЯпlЃЌЪЙЕУS1=ІЫS2 ЃЌ ЩшГіжБЯпЗНГЬЃЌгЩЕуЕНжБЯпЕФОрРыЙЋЪНЧѓГіMКЭNЕНжБЯпlЕФОрРыЃЌРћгУЪ§бЇзЊЛЏЫМЯыАбСНИіШ§НЧаЮЕФУцЛ§БШзЊЛЏЮЊЯпЖЮГЄЖШБШЃЌгЩЯвГЄЙЋЪНЕУЕНЯпЖЮГЄЖШБШЕФСэвЛБэДяЪНЃЌСНЪНЯрЕШЕУЕН ![]() ЃЌЛЛдЊКѓРћгУЗЧСуЕФkжЕДцдкЬжТлІЫЕФШЁжЕЗЖЮЇЃЎ
ЃЌЛЛдЊКѓРћгУЗЧСуЕФkжЕДцдкЬжТлІЫЕФШЁжЕЗЖЮЇЃЎ
ЁОПМЕуОЋЮіЁПЙигкБОЬтПМВщЕФЕуЕНжБЯпЕФОрРыЙЋЪНЃЌашвЊСЫНтЕу![]() ЕНжБЯп
ЕНжБЯп![]() ЕФОрРыЮЊЃК
ЕФОрРыЮЊЃК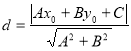 ВХФмЕУГіе§ШЗД№АИЃЎ
ВХФмЕУГіе§ШЗД№АИЃЎ

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИЁОЬтФПЁПФГжабЇвЛУћЪ§бЇРЯЪІЖдШЋАр50УћбЇЩњФГДЮПМЪдГЩМЈЗжФаХЎЩњНјааЭГМЦЃЈТњЗж150ЗжЃЉЃЌЦфжа120ЗжЃЈКЌ120ЗжЃЉвдЩЯЮЊгХауЃЌЛцжЦСЫШчЭМЫљЪОЕФСНИіЦЕТЪЗжВМжБЗНЭМЃК

ЃЈ1ЃЉИљОнвдЩЯСНИіжБЗНЭМЭъГЩЯТУцЕФ![]() СаСЊБэЃК
СаСЊБэЃК
адБ№ ГЩМЈ | гХау | ВЛгХау | змМЦ |
ФаЩњ | |||
ХЎЩњ | |||
змМЦ |
ЃЈ2ЃЉИљОнЃЈ1ЃЉжаБэИёЕФЪ§ОнМЦЫуЃЌФугаЖрДѓАбЮеШЯЮЊбЇЩњЕФЪ§бЇГЩМЈгыадБ№жЎМфгаЙиЯЕЃП
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
ИНЃК![]() ЃЌЦфжа
ЃЌЦфжа![]() .
.
ЁОЬтФПЁПМзЁЂввСНИіРКЧђЖгдк4ДЮВЛЭЌБШШќжаЕФЕУЗжЧщПіШчЯТЃК
МзЖг | 88 | 91 | 92 | 96 |
ввЖг | 89 | 93 | 9Ј | 92 |
ввЖгМЧТМжагавЛИіЪ§зжФЃК§ЃЈМДБэжавѕгАВПЗжЃЉЃЌЮоЗЈШЗШЯЃЌМйЩшетИіЪ§зжОпгаЫцЛњадЃЌВЂгУ![]() БэЪО.
БэЪО.
ЃЈЂёЃЉдк4ДЮБШШќжаЃЌЧѓввЖгЦНОљЕУЗжГЌЙ§МзЖгЦНОљЕУЗжЕФИХТЪЃЛ
ЃЈЂђЃЉЕБ![]() ЪБЃЌЗжБ№ДгМзЁЂввСНЖгЕФ4ДЮБШШќжаИїЫцЛњбЁШЁ1ДЮЃЌМЧет2ИіБШШќЕУЗжжЎВюЕФОјЖджЕЮЊ
ЪБЃЌЗжБ№ДгМзЁЂввСНЖгЕФ4ДЮБШШќжаИїЫцЛњбЁШЁ1ДЮЃЌМЧет2ИіБШШќЕУЗжжЎВюЕФОјЖджЕЮЊ![]() ЃЌЧѓЫцЛњБфСП
ЃЌЧѓЫцЛњБфСП![]() ЕФЗжВМСаЃЛ
ЕФЗжВМСаЃЛ
ЃЈЂѓЃЉШчЙћввЖгЕУЗжЪ§ОнЕФЗНВюВЛаЁгкМзЖгЕУЗжЪ§ОнЕФЗНВюЃЌаДГі![]() ЕФШЁжЕМЏКЯ.(НсТлВЛвЊЧѓжЄУїЃЉ
ЕФШЁжЕМЏКЯ.(НсТлВЛвЊЧѓжЄУїЃЉ
ЁОЬтФПЁПЯжааЕФИіЫАЗЈаое§АИЙцЖЈЃКИіЫАУтеїЖюгЩдРДЕФ2000дЊЬсИпЕН3500дЊЃЌВЂИјГіСЫаТЕФИіШЫЫљЕУЫАЫАТЪБэЃК
ШЋдТгІФЩЫАЫљЕУЖю | ЫАТЪ |
ВЛГЌЙ§1500дЊЕФВПЗж | 3% |
ГЌЙ§1500дЊжС4500дЊЕФВПЗж | 10% |
ГЌЙ§4500дЊжС9000дЊЕФВПЗж | 20% |
ГЌЙ§9000дЊжС35000дЊЕФВПЗж | 25% |
ЁЁ | Ё |
Р§ШчФГШЫЕФдТЙЄзЪЪеШыЮЊ5000дЊЃЌФЧУДЫћгІФЩИіШЫЫљЕУЫАЮЊЃК![]() ЃЈдЊЃЉ.
ЃЈдЊЃЉ.
ЃЈЂёЃЉШєМзЕФдТЙЄзЪЪеШыЮЊ6000дЊЃЌЧѓМзгІФЩЕФИіШЫЪеЕФЫАЃЛ
ЃЈЂђЃЉЩшввЕФдТЙЄзЪЪеШыЮЊ![]() дЊЃЌгІФЩИіШЫЫљЕУЫАЮЊ
дЊЃЌгІФЩИіШЫЫљЕУЫАЮЊ![]() дЊЃЌЧѓ
дЊЃЌЧѓ![]() Йигк
Йигк![]() ЕФКЏЪ§ЃЛ
ЕФКЏЪ§ЃЛ
ЃЈЂѓЃЉШєБћФГдТгІФЩЕФИіШЫЫљЕУЫАЮЊ1000дЊЃЌИјГіБћЕФдТЙЄзЪЪеШы.ЃЈНсТлВЛвЊЧѓжЄУїЃЉ



