��Ŀ����
����Ŀ���ס��������������4�β�ͬ�����еĵ÷�������£�
�� | 88 | 91 | 92 | 96 |
�Ҷ� | 89 | 93 | 9�� | 92 |
�ҶӼ�¼����һ������ģ������������Ӱ���֣�����ȷ�ϣ�����������־�������ԣ�����![]() ��ʾ.
��ʾ.
������4�α����У����Ҷ�ƽ���÷ֳ�����ƽ���÷ֵĸ��ʣ�
����![]() ʱ���ֱ�Ӽס������ӵ�4�α����и����ѡȡ1�Σ�����2�������÷�֮��ľ���ֵΪ
ʱ���ֱ�Ӽס������ӵ�4�α����и����ѡȡ1�Σ�����2�������÷�֮��ľ���ֵΪ![]() �����������
�����������![]() �ķֲ��У�
�ķֲ��У�
��������Ҷӵ÷����ݵķ��С�ڼӵ÷����ݵķ��д��![]() ��ȡֵ����.(���۲�Ҫ��֤����
��ȡֵ����.(���۲�Ҫ��֤����
���𰸡�����![]() �����ֲ��м�����������
�����ֲ��м�����������![]() .
.
���������������������ݱ������ݣ�д��![]() ��ȫ�����ܣ���ס��Ҷӵ�ƽ���ɼ����г�����
��ȫ�����ܣ���ס��Ҷӵ�ƽ���ɼ����г�����![]() �IJ���ʽ�����
�IJ���ʽ�����![]() ��ȡֵ���ϣ����ɹŵ���͵ĸ��ʼ��㹫ʽ�����.
��ȡֵ���ϣ����ɹŵ���͵ĸ��ʼ��㹫ʽ�����.
����2�������÷�֮��ľ���ֵ![]() ������ȡֵΪ0��1��2��3��4��5��7�������Ӧ���ʣ���������������
������ȡֵΪ0��1��2��3��4��5��7�������Ӧ���ʣ���������������![]() �ķֲ���.
�ķֲ���.
����д���ס������ӵķ���г�����![]() �IJ���ʽ���������
�IJ���ʽ���������![]() ��ȡֵ����.
��ȡֵ����.
��������������������Ҷ�ƽ���÷ֳ�����ƽ���÷���Ϊ�¼�![]() ,
,
������![]() ������10�ֿ���.
������10�ֿ���.
���Ҷ�ƽ���÷ֳ�����ƽ���÷֣���![]()
���![]()
���Ե�![]() ʱ���Ҷ�ƽ���÷ֳ�����ƽ���÷֣���6�ֿ���.
ʱ���Ҷ�ƽ���÷ֳ�����ƽ���÷֣���6�ֿ���.
�����Ҷ�ƽ���÷ֳ�����ƽ���÷ֵĸ���Ϊ![]()
��������![]() ʱ���Ǽӵ�4�α����÷�88��91��92��96�ֱ�Ϊ
ʱ���Ǽӵ�4�α����÷�88��91��92��96�ֱ�Ϊ![]() ���Ҷӵ�4�α����÷�89��93��95��92�ֱ�Ϊ
���Ҷӵ�4�α����÷�89��93��95��92�ֱ�Ϊ![]()
��ֱ�Ӽס������ӵ�4�α����и����ѡȡ1�Σ����п��ܵĵ÷ֽ����![]() �֣�������
�֣�������![]()
![]()
����2�������÷�֮��ľ���ֵΪ![]() ������ȡֵΪ0��1��2��3��4��5��7.
������ȡֵΪ0��1��2��3��4��5��7.
���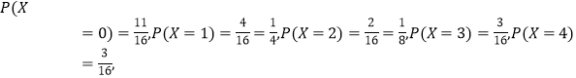
![]()
�����������![]() �ķֲ�Ϊ��
�ķֲ�Ϊ��
| 0 | 1 | 2 | 3 | 4 | 5 | 7 |
|
|
|
|
|
|
|
|
(��![]()

 ͬ��ѧ��һ�ζ���ϵ�д�
ͬ��ѧ��һ�ζ���ϵ�д� �����ܾ�ϵ�д�
�����ܾ�ϵ�д� ���ƿ�����ϵ�д�
���ƿ�����ϵ�д� ���¿쳵����������ϵ�д�
���¿쳵����������ϵ�д�����Ŀ����ij���鼮ÿ��ijɱ���![]() ��Ԫ����ӡˢ����
��Ԫ����ӡˢ����![]() ��ǧ�ᣩ���������˳����������õ������ɢ��ͼ��һЩͳ������ֵ.
��ǧ�ᣩ���������˳����������õ������ɢ��ͼ��һЩͳ������ֵ.

|
|
|
|
|
|
|
4.83 | 4.22 | 0.3775 | 60.17 | 0.60 | -39.38 | 4.8 |
����![]() ��
��![]() .
.
Ϊ��Ԥ��ӡˢ20ǧ��ʱÿ��ijɱ��ѣ������������ع�ģ�ͣ�![]() ��
��![]() .
.
��1������ɢ��ͼ������Ϊѡ���ĸ�ģ��Ԥ����ɿ�����ֻѡ��ģ�ͼ��ɣ�
��2�������������ݺͣ�1����ѡ���ģ�ͣ���![]() ����
����![]() �Ļع鷽�̣���Ԥ��ӡˢ20ǧ��ʱÿ��ijɱ���.
�Ļع鷽�̣���Ԥ��ӡˢ20ǧ��ʱÿ��ijɱ���.
��������һ������![]() ��
��![]() ������
������![]() ����ع鷽��
����ع鷽��![]() ��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ��
��б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ�� ��
��![]() .
.