题目内容
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的焦点为
的焦点为![]() ,点
,点![]() 是抛物线
是抛物线![]() 上一点,且
上一点,且![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 为抛物线
为抛物线![]() 上异于
上异于![]() 的两点,且
的两点,且![]() .记点
.记点![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】分析:(1)利用抛物线的定义求p的值.(2)先求出a的值,再联立直线的方程和抛物线的方程得到韦达定理,再求![]() |(y1+2) (y2+2)|的值.
|(y1+2) (y2+2)|的值.
详解:(1)因为点A(1,a) (a>0)是抛物线C上一点,且AF=2,
所以![]() +1=2,所以p=2.
+1=2,所以p=2.
(2)由(1)得抛物线方程为y2=4x.
因为点A(1,a) (a>0)是抛物线C上一点,所以a=2.
设直线AM方程为x-1=m (y-2) (m≠0),M(x1,y1),N(x2,y2).
由![]() 消去x,得y2-4m y+8m-4=0,
消去x,得y2-4m y+8m-4=0,
即(y-2)( y-4m+2)=0,所以y1=4m-2.
因为AM⊥AN,所以-![]() 代m,得y2=-
代m,得y2=-![]() -2,
-2,
所以d1d2=|(y1+2) (y2+2)|=|4m×(-![]() )|=16.
)|=16.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
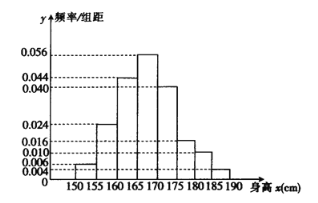
小学生10分钟应用题系列答案【题目】涡阳县某华为手机专卖店对市民进行华为手机认可度的调查,在已购买华为手机的![]() 名市民中,随机抽取
名市民中,随机抽取![]() 名,按年龄(单位:岁)进行统计的频数分布表和频率分布直方图如图:
名,按年龄(单位:岁)进行统计的频数分布表和频率分布直方图如图:

分组(岁) | 频数 |
|
|
|
|
|
|
|
|
|
|
合计 |
|
(1)求频数分布表中![]() 、
、![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)在抽取的这![]() 名市民中,从年龄在
名市民中,从年龄在![]() 、
、![]() 内的市民中用分层抽样的方法抽取
内的市民中用分层抽样的方法抽取![]() 人参加华为手机宣传活动,现从这
人参加华为手机宣传活动,现从这![]() 人中随机选取
人中随机选取![]() 人各赠送一部华为手机,求这
人各赠送一部华为手机,求这![]() 人中恰有
人中恰有![]() 人的年龄在
人的年龄在![]() 内的概率.
内的概率.
【题目】某餐厅通过查阅了最近5次食品交易会参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下统计表:
(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
(1)根据所给5组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)已知购买原材料的费用![]() (元)与数量
(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,
,
投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有15万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润![]() 销售收入
销售收入![]() 原材料费用).
原材料费用).
参考公式:  ,
, ![]() .
.
参考数据: ![]() ,
, ![]() ,
, ![]() .
.