题目内容
20.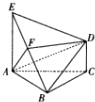 如图,在多面体ABCDE中,EA⊥平面ABC,DC∥EA且EA=2DC,CA=CB,F为BE的中点.
如图,在多面体ABCDE中,EA⊥平面ABC,DC∥EA且EA=2DC,CA=CB,F为BE的中点.(1)求证:DF∥平面ABC;
(2)求证:平面ADF⊥平面ABE.
分析 (1)根据线面平行的判定定理证明FD∥CG即可证明DF∥平面ABC;
(2)根据面面垂直的判定定理即即可证明平面ADF⊥平面ABE
解答 (1)证明:如图所示,取AB中点G,连CG、FG.
∵F为BE的中点.
∴EF=FB,AG=GB,
∴FG∥EA且FG=$\frac{1}{2}$EA.
又DC∥EA,CD=$\frac{1}{2}$EA,
∴GF∥DC且GF=DC.
∴四边形CDFG为平行四边形,
∴FD∥CG.
∵DF?平面ABC,CG?平面ABC,
∴DF∥平面ABC.
(2)证明:△ABC中,CA=CB.G是AB的中点,
∴CG⊥AB
∵EA⊥平面ABC,CG?平面ABC,
∴AE⊥CG.
∵AB∩EA=A,AB?平面AEB,EA?平面AEB
∴CG⊥平面AEB.
又∵DF∥CG,
∴DF⊥平面AEB.DF?平面BDE
∴平面ADF⊥平面ABE.
点评 本题主要考查空间面面垂直以及线面平行的判定,根据相应的判定定理是解决本题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
10.一个几何体的三视图如图所示,则该几何体的表面积为( )


| A. | 6π | B. | 7π | C. | 8π | D. | 9π |
15.下列命题中:
①若a∈R,则ai是纯虚数;
②若a,b∈R且a>b,则a+i4>b+i2;
③复数2+i的模为3;
④两个虚数不能比较大小.
其中,正确命题的序号是( )
①若a∈R,则ai是纯虚数;
②若a,b∈R且a>b,则a+i4>b+i2;
③复数2+i的模为3;
④两个虚数不能比较大小.
其中,正确命题的序号是( )
| A. | ①② | B. | ②④ | C. | ②③ | D. | ①④ |
12.已知角α的终边经过点P(-b,4)且cosα=-$\frac{3}{5}$,则b的值等于( )
| A. | 3 | B. | -3 | C. | ±3 | D. | 5 |
 圆柱形容器盛有为8cm的水,现放入三个相同的玻璃小球(小球的半径与圆柱的底面半径相等),若水刚好淹没最上方的小球,如图所示,则小球的半径为4.
圆柱形容器盛有为8cm的水,现放入三个相同的玻璃小球(小球的半径与圆柱的底面半径相等),若水刚好淹没最上方的小球,如图所示,则小球的半径为4.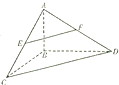 如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥BD,AB=3,BC=BD=4,点E,F分别是AC,AD的中点
如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥BD,AB=3,BC=BD=4,点E,F分别是AC,AD的中点