题目内容
17.已知函数f(x)=($\frac{1}{a}$)2-2x(a>0,a≠1)的图象恒经过与a无关的定点A,(1)求点A的坐标
(2)若偶函数g(x)=ax2+bx-c,x∈[1-2c,c]的图象过点A,求a,b,c的值.
分析 (1)由指数函数的性质得,令2-2x=0即可;
(2)由题意知1-2c+c=0,b=0,g(1)=1,从而解得.
解答 解:(1)令2-2x=0得,x=1,
此时f(1)=1,
故A(1,1);
(2)∵g(x)是偶函数,
∴1-2c+c=0,b=0;
∴c=1,b=0;
故g(x)=ax2-1,
又∵g(1)=a-1=1,
∴a=2;
故a=2,b=0,c=1.
点评 本题考查了指数函数与二次函数的性质应用,属于基础题.

练习册系列答案
相关题目
12.已知角α的终边经过点P(-b,4)且cosα=-$\frac{3}{5}$,则b的值等于( )
| A. | 3 | B. | -3 | C. | ±3 | D. | 5 |
2.在如图所示的四个图示中,是结构图的是( )
| A. | 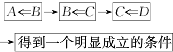 | B. | 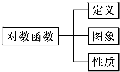 | ||
| C. | 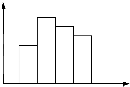 | D. | 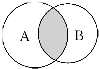 |
6.“$\frac{1}{a}$>1”是“函数f(x)=(3-2a)x单调递增”( )
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充分且必要 | D. | 既不充分也不必要 |
7.定义:$\frac{n}{{p}_{1}+{p}_{1}+…+{p}_{n}}$为n个p1,p2,…pn的“均倒数”,若已知正数数列{an}的前n项的”均倒数“为$\frac{1}{2n+1}$,又bn=$\frac{{a}_{n}-1}{2}$.,$\frac{1}{{b}_{1}{b}_{2}}$+$\frac{1}{{b}_{2}{b}_{3}}$+…+$\frac{1}{{b}_{2014}{b}_{2015}}$=( )
| A. | $\frac{2013}{4027}$ | B. | $\frac{4026}{4027}$ | C. | $\frac{2014}{4029}$ | D. | $\frac{4028}{4029}$ |
 圆柱形容器盛有为8cm的水,现放入三个相同的玻璃小球(小球的半径与圆柱的底面半径相等),若水刚好淹没最上方的小球,如图所示,则小球的半径为4.
圆柱形容器盛有为8cm的水,现放入三个相同的玻璃小球(小球的半径与圆柱的底面半径相等),若水刚好淹没最上方的小球,如图所示,则小球的半径为4.