题目内容
18.要得到函数y=tan(3x+$\frac{π}{3}$)的图象,只须将x=tan3x的图象上的所有的点( )| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{π}{9}$个单位长度 | D. | 向右平移$\frac{π}{9}$个单位长度 |
分析 由条件利用函数的图象的平移变换规律,可得结论.
解答 解:将x=tan3x的图象上的所有的点向左平移$\frac{π}{9}$个单位长度,即可得到函数y=tan3(x+$\frac{π}{9}$)=tan(3x+$\frac{π}{3}$)的图象,
故选:C.
点评 本题主要考查函数的图象的平移变换规律,属于基础题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
6.“$\frac{1}{a}$>1”是“函数f(x)=(3-2a)x单调递增”( )
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充分且必要 | D. | 既不充分也不必要 |
3.b,c表示两条不重合的直线,α,β表示两个不重合的平面,下列命题中正确的是( )
| A. | $\left.\begin{array}{l}{c∥α}\\{b?α}\end{array}\right\}$⇒c∥b | B. | $\left.\begin{array}{l}{c∥α}\\{α⊥β}\end{array}\right\}$⇒c⊥β | C. | $\left.\begin{array}{l}{c⊥α}\\{c⊥β}\end{array}\right\}$⇒α∥β | D. | $\left.\begin{array}{l}{b∥c}\\{c?α}\end{array}\right\}$⇒b∥α |
7.定义:$\frac{n}{{p}_{1}+{p}_{1}+…+{p}_{n}}$为n个p1,p2,…pn的“均倒数”,若已知正数数列{an}的前n项的”均倒数“为$\frac{1}{2n+1}$,又bn=$\frac{{a}_{n}-1}{2}$.,$\frac{1}{{b}_{1}{b}_{2}}$+$\frac{1}{{b}_{2}{b}_{3}}$+…+$\frac{1}{{b}_{2014}{b}_{2015}}$=( )
| A. | $\frac{2013}{4027}$ | B. | $\frac{4026}{4027}$ | C. | $\frac{2014}{4029}$ | D. | $\frac{4028}{4029}$ |
8.设集合A={x|x2-6x+8<0},B={x|2<2x<8},则A∩B=( )
| A. | {x|1<x<4} | B. | {x|1<x<3} | C. | {x|2<x<3} | D. | {x|3<x<4} |
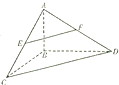 如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥BD,AB=3,BC=BD=4,点E,F分别是AC,AD的中点
如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥BD,AB=3,BC=BD=4,点E,F分别是AC,AD的中点