题目内容
4．已知双曲线的左、右焦点分别为F1，F2，在左支上过F1的弦AB的长为10，若2a=16，则△ABF2的周长是（ ）| A． | 32 | B． | 36 | C． | 42 | D． | 52 |
分析 由双曲线的定义可得AF2+BF2 =42，△ABF2的周长是（ AF1 +AF2 ）+（ BF1+BF2 ）=（AF2+BF2 ）+AB，计算可得答案．
解答 解：由双曲线的定义可得 AF2-AF1=2a，BF2 -BF1=2a，
∴AF2+BF2 -AB=4a=32，即AF2+BF2 -10=32，AF2+BF2 =42．
△ABF2（F2为右焦点）的周长是 （ AF1 +AF2 ）+（ BF1+BF2 ）=（AF2+BF2 ）+AB=42+10=52．
故选：D．
点评 本题考查双曲线的定义和双曲线的标准方程，以及双曲线的简单性质的应用，求出AF2+BF2 =42是解题的关键．
练习册系列答案
相关题目
15．下列命题中：
①若a∈R，则ai是纯虚数；
②若a，b∈R且a＞b，则a+i4＞b+i2；
③复数2+i的模为3；
④两个虚数不能比较大小．
其中，正确命题的序号是（ ）
①若a∈R，则ai是纯虚数；
②若a，b∈R且a＞b，则a+i4＞b+i2；
③复数2+i的模为3；
④两个虚数不能比较大小．
其中，正确命题的序号是（ ）
| A． | ①② | B． | ②④ | C． | ②③ | D． | ①④ |
12．已知角α的终边经过点P（-b，4）且cosα=-$\frac{3}{5}$，则b的值等于（ ）
| A． | 3 | B． | -3 | C． | ±3 | D． | 5 |
正方形ABCD与正方形ABEF互相垂直，点M，N，G分别是AE，BC，CE的中点，AB=2，
14．
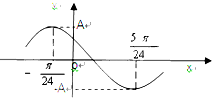已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），其部分图象如下图所示，且直线y=A与曲线y=f（x）（-$\frac{π}{24}$$≤x≤\frac{11π}{24}$）所围成的封闭图形的面积为π，则f（$\frac{π}{8}$）+f（$\frac{2π}{8}$）+f（$\frac{3π}{8}$）+…+f（$\frac{2015π}{8}）$的值为（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），其部分图象如下图所示，且直线y=A与曲线y=f（x）（-$\frac{π}{24}$$≤x≤\frac{11π}{24}$）所围成的封闭图形的面积为π，则f（$\frac{π}{8}$）+f（$\frac{2π}{8}$）+f（$\frac{3π}{8}$）+…+f（$\frac{2015π}{8}）$的值为（ ）| A． | -$\sqrt{3}$ | B． | -1-$\sqrt{3}$ | C． | $\sqrt{3}$ | D． | -1+$\sqrt{3}$ |