题目内容

19．曲线$y=\frac{x+1}{x-1}$在点（3，2）处的切线的方程为x+2y-7=0．

分析 由题意求出导数：y′=$\frac{-2}{{（x-1）}^{2}}$，进而根据切点坐标求出切线的斜率，即可求出切线的方程．

解答 解：由题意可得：y′=$\frac{-2}{{（x-1）}^{2}}$，
所以在点（3，2）处的切线斜率为-$\frac{1}{2}$，
所以在点（3，2）处的切线方程为：y=-$\frac{1}{2}$（x-3）+2．
即x+2y-7=0
故答案为：x+2y-7=0．

点评 此题考查学生熟练利用导数求曲线上过某点切线方程的斜率，能够根据一点坐标和斜率写出直线的方程，是一道基础题．

练习册系列答案
相关题目
9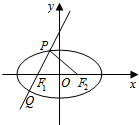．已知椭圆E的左、右焦点分别为F1、F2，过F1且斜率为2的直线交椭圆E于P、Q两点，若△PF1F2为直角三角形，则椭圆E的离心率为（　　）
A．$\frac{\sqrt{5}}{3}$B．$\frac{2}{3}$C．$\frac{\sqrt{2}}{3}$D．$\frac{1}{3}$
10．一个几何体的三视图如图所示，则该几何体的表面积为（　　）
A．6πB．7πC．8πD．9π
7．在三棱柱ABC-A1B1C1中，△ABC为正三角形，AA1⊥底面ABC，E是AB的中点，F是BC1的中点．下列命题正确的是①②③⑤（写出所有正确命题的编号）．
①EF∥平面ACC1A1；
②平面CEF⊥平面 ABB1A1；
③平面CEF截该三棱柱所得大小两部分的体积比为11：1；
④若该三棱柱有内切球，则AB=$\sqrt{3}$BB1；
⑤若BB1上有唯一点G，使得A1G⊥CG，则BB1=$\sqrt{2}$AB．
14．已知数列{an}的前n项和为Sn，且Sn=n（n+1）．
（1）求数列{an}的通项公式an；
（Ⅱ）数列{bn}的通项公式bn=$\frac{1}{{a}_{n}•{a}_{n+2}}$，其前n项和为Tn，求证：${T_n}＜\frac{3}{16}$．
4．已知点A（-2，0），B（0，-2），C（2sinθ，cosθ）．
（Ⅰ）若|$\overrightarrow{AC}$|=|$\overrightarrow{BC}$|，求tanθ和$\frac{3sinθ-4cosθ}{4cosθ+3sinθ}$的值；
（Ⅱ）若（$\overrightarrow{OA}$+2$\overrightarrow{OB}$）•$\overrightarrow{OC}$=1，其中O为坐标原点，求sinθ•cosθ的值．
11．以直角坐标系的原点为极点，x轴正半轴为极轴，并在两种坐标系中取相同的长度单位，已知直线l的极坐标方程为ρsin（θ-$\frac{π}{3}$）=6，圆C的参数方程为$\left\{\begin{array}{l}{x=10cosθ}\\{y=10sinθ}\end{array}\right.$，（θ为参数）．
（1）求直线l的直角坐标方成；
（2）求直线l被圆截得得弦长．
8．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的一个顶点为A（0，1），离心为$\frac{\sqrt{2}}{2}$，过点B（0，-2）及左焦点F1的直线交椭圆于C、D两点，右焦点为F2．
求：（1）椭圆的方程；
（2）三角形CDF2的面积．
9．命题p：已知f（x）=x2+（m2-1）x+（m-2）的一个零点比1大，一个零点比1小．
命题q：$\frac{1}{{m}^{2}}$-4m2≤-$\frac{3}{{x}^{2}}$-$\frac{2}{x}$+1在x∈[$\frac{3}{2}$，+∞）上恒成立．
若￢p为假命题，p∧q为真命题，求m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网