题目内容
19.已知椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左右焦点为F1,F2,点A(x1,y1),B(x2,y2)在椭圆上,若x1+x2=$\frac{1}{2}$,且$\overrightarrow{A{F}_{2}}$=λ$\overrightarrow{{F}_{2}B}$,求λ的值.分析 利用椭圆的第二定义,结合向量知识,列出关系式,即可求出λ的值.
解答 解:由椭圆的第二定义,可得|AF2|=2-$\frac{1}{2}$x1,|BF2|=2-$\frac{1}{2}$x2,
∵$\overrightarrow{A{F}_{2}}$=λ$\overrightarrow{{F}_{2}B}$,
∴2-$\frac{1}{2}$x1=λ(2-$\frac{1}{2}$x2),x1-1=λ(1-x2)
∵x1+x2=$\frac{1}{2}$,
联立可得λ=$\frac{3±\sqrt{5}}{2}$.
点评 本题主要考查了椭圆的简单性质,考查了学生对椭圆定义的理解和运用.

练习册系列答案
相关题目
7.定义:$\frac{n}{{p}_{1}+{p}_{1}+…+{p}_{n}}$为n个p1,p2,…pn的“均倒数”,若已知正数数列{an}的前n项的”均倒数“为$\frac{1}{2n+1}$,又bn=$\frac{{a}_{n}-1}{2}$.,$\frac{1}{{b}_{1}{b}_{2}}$+$\frac{1}{{b}_{2}{b}_{3}}$+…+$\frac{1}{{b}_{2014}{b}_{2015}}$=( )
| A. | $\frac{2013}{4027}$ | B. | $\frac{4026}{4027}$ | C. | $\frac{2014}{4029}$ | D. | $\frac{4028}{4029}$ |
14.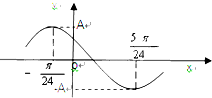 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如下图所示,且直线y=A与曲线y=f(x)(-$\frac{π}{24}$$≤x≤\frac{11π}{24}$)所围成的封闭图形的面积为π,则f($\frac{π}{8}$)+f($\frac{2π}{8}$)+f($\frac{3π}{8}$)+…+f($\frac{2015π}{8})$的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如下图所示,且直线y=A与曲线y=f(x)(-$\frac{π}{24}$$≤x≤\frac{11π}{24}$)所围成的封闭图形的面积为π,则f($\frac{π}{8}$)+f($\frac{2π}{8}$)+f($\frac{3π}{8}$)+…+f($\frac{2015π}{8})$的值为( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如下图所示,且直线y=A与曲线y=f(x)(-$\frac{π}{24}$$≤x≤\frac{11π}{24}$)所围成的封闭图形的面积为π,则f($\frac{π}{8}$)+f($\frac{2π}{8}$)+f($\frac{3π}{8}$)+…+f($\frac{2015π}{8})$的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如下图所示,且直线y=A与曲线y=f(x)(-$\frac{π}{24}$$≤x≤\frac{11π}{24}$)所围成的封闭图形的面积为π,则f($\frac{π}{8}$)+f($\frac{2π}{8}$)+f($\frac{3π}{8}$)+…+f($\frac{2015π}{8})$的值为( )| A. | -$\sqrt{3}$ | B. | -1-$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | -1+$\sqrt{3}$ |
4.已知函数f(x)满足f(x+4)=f(x),且当-1<x≤3时,f(x)=$\left\{\begin{array}{l}{m\sqrt{1-{x}^{2}},x∈(-1,1]}\\{1-|x-2|,x∈(1,3]}\end{array}\right.$.其中m>0,若方程3f(x)-x=0恰好有5个根,则实数m的取值范围是( )
| A. | ($\frac{\sqrt{15}}{3}$,$\sqrt{7}$) | B. | ($\frac{\sqrt{15}}{3}$,$\frac{8}{3}$) | C. | ($\frac{4}{3}$,$\sqrt{7}$) | D. | ( $\frac{4}{3}$,$\frac{8}{3}$) |
8.设集合A={x|x2-6x+8<0},B={x|2<2x<8},则A∩B=( )
| A. | {x|1<x<4} | B. | {x|1<x<3} | C. | {x|2<x<3} | D. | {x|3<x<4} |
9.甲、乙两人在2015年1月至5月的纯收入(单位:千元)的数据如下表:
(1)由表中数据直观分析,甲、乙两人中谁的纯收入较稳定?
(2)求y关于x的线性回归方程,并预测甲在6月份的纯收入;
(3)现从乙这5个月的纯收入中,随机抽取两个月,求恰有1个月的纯收入在区间(3,3.5)中的概率.
| 月份x | 1 | 2 | 3 | 4 | 5 |
| 甲的纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 |
| 乙的纯收入z | 2.8 | 3.4 | 3.8 | 4.5 | 5.5 |
(2)求y关于x的线性回归方程,并预测甲在6月份的纯收入;
(3)现从乙这5个月的纯收入中,随机抽取两个月,求恰有1个月的纯收入在区间(3,3.5)中的概率.
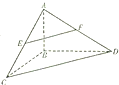 如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥BD,AB=3,BC=BD=4,点E,F分别是AC,AD的中点
如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥BD,AB=3,BC=BD=4,点E,F分别是AC,AD的中点