题目内容
11.若关于x的不等式(3x-1)2<ax2的解集中恰有2个整数,则实数a的取值范围是($\frac{25}{4}$,$\frac{64}{9}$].分析 由不等式可知a是大于0,(3x-1)2<ax2即为ax2-(3x-1)2>0.利用平方差分解因式得[($\sqrt{a}$+3)x-1][($\sqrt{a}$-3)x+1]>0,得到a的解集,由解集中的整数恰有2个,且为1,2,得到a的不等式,解不等式可得a的范围.
解答 解:由题知,a>0 则
(3x-1)2<ax2即为ax2-(3x-1)2>0.
即($\sqrt{a}$x+3x-1)($\sqrt{a}$x-3x+1)>0,
即[($\sqrt{a}$+3)x-1][($\sqrt{a}$-3)x+1]>0,
由于$\sqrt{a}$+3>0,而不等式的解答中恰有两个整数解,
故必有$\sqrt{a}$-3<0,即必有a<9,
所以不等式可变为[($\sqrt{a}$+3)x-1][(3-$\sqrt{a}$)x-1]<0,
解得$\frac{1}{\sqrt{a}+3}$<x<$\frac{1}{3-\sqrt{a}}$,
又0<$\frac{1}{\sqrt{a}+3}$<1,结合解集中恰有两个整数,即为1,2.
可得2<$\frac{1}{3-\sqrt{a}}$≤3,
解得$\frac{25}{4}$<a≤$\frac{64}{9}$.
所以a∈($\frac{25}{4}$,$\frac{64}{9}$].
故答案为:($\frac{25}{4}$,$\frac{64}{9}$].
点评 本题考查学生解含参一元二次不等式的能力,运用一元二次不等式解决数学问题的能力.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
16.已知某校的体育场东侧有4个门,西侧有4个门,某同学要去体育场晨练,则他进出门的方案有( )
| A. | 16种 | B. | 8种 | C. | 32种 | D. | 64种 |
20.复数3-i在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,已知
,已知 ,
, .
. ,
, ,
, 成等差数列时,求
成等差数列时,求 为
为 边的中点,求线段
边的中点,求线段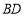 长的最小值.
长的最小值.