题目内容
12.已知一圆锥的底面是半径为1cm的圆,若圆锥的侧面积是底面积的3倍,则该圆锥的体积是$\frac{2\sqrt{2}π}{3}$cm3.分析 由已知中,圆锥的底面半径为1,侧面积是底面积的3倍,分析圆锥的母线长,进而求出圆锥的高,结合圆锥的体积公式即可获得问题的解答.
解答 解:∵圆锥的底面半径r=1cm,侧面积是底面积的3倍,
∴圆锥的母线长l=3cm,
故圆锥的高h=$\sqrt{{l}^{2}-{r}^{2}}$=2$\sqrt{2}$cm,
故圆锥的体积V=$\frac{1}{3}$Sh=$\frac{1}{3}$πr2•h=$\frac{1}{3}×{1}^{2}π×2\sqrt{2}$=$\frac{2\sqrt{2}π}{3}$cm3,
故答案为:$\frac{2\sqrt{2}π}{3}$.
点评 本题考查的是圆锥的体积求解问题.在解答的过程当中充分体现了圆锥体积公式的应用以及转化思想的应用.值得同学们体会反思.

练习册系列答案
相关题目
20.复数3-i在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.椭圆$\frac{x^2}{5}+\frac{y^2}{9}=1$的焦距是( )
| A. | 4 | B. | $\sqrt{14}$ | C. | 8 | D. | $2\sqrt{14}$ |
2.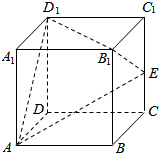 在棱长为1的正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内(包括边)的动点,且A1F∥平面D1AE,沿A1F运动,将B1点所在的几何体削去,则剩余几何体的体积为( )
在棱长为1的正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内(包括边)的动点,且A1F∥平面D1AE,沿A1F运动,将B1点所在的几何体削去,则剩余几何体的体积为( )
 在棱长为1的正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内(包括边)的动点,且A1F∥平面D1AE,沿A1F运动,将B1点所在的几何体削去,则剩余几何体的体积为( )
在棱长为1的正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内(包括边)的动点,且A1F∥平面D1AE,沿A1F运动,将B1点所在的几何体削去,则剩余几何体的体积为( )| A. | $\frac{3}{4}$ | B. | $\frac{7}{8}$ | C. | $\frac{11}{12}$ | D. | $\frac{23}{24}$ |