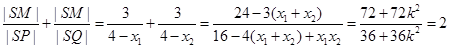题目内容
线段 是椭圆
是椭圆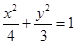 过
过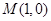 的一动弦,且直线
的一动弦,且直线 与直线
与直线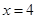 交于点
交于点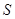 ,则
,则
 是椭圆
是椭圆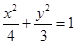 过
过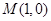 的一动弦,且直线
的一动弦,且直线 与直线
与直线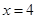 交于点
交于点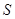 ,则
,则
2
依题意可得,点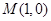 是椭圆的右焦点,直线
是椭圆的右焦点,直线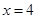 是椭圆的右准线,而
是椭圆的右准线,而 。可知直线
。可知直线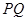 的斜率存在,设其方程为
的斜率存在,设其方程为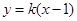 。联立
。联立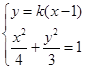 可得
可得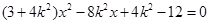 ,设
,设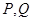 坐标为
坐标为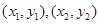 ,则
,则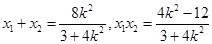 。根据椭圆的第二定义可得,
。根据椭圆的第二定义可得,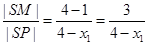 ,
,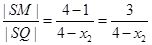 ,所以
,所以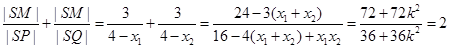
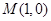 是椭圆的右焦点,直线
是椭圆的右焦点,直线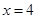 是椭圆的右准线,而
是椭圆的右准线,而 。可知直线
。可知直线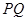 的斜率存在,设其方程为
的斜率存在,设其方程为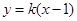 。联立
。联立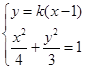 可得
可得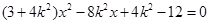 ,设
,设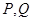 坐标为
坐标为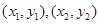 ,则
,则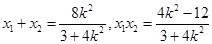 。根据椭圆的第二定义可得,
。根据椭圆的第二定义可得,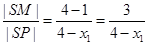 ,
,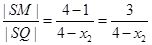 ,所以
,所以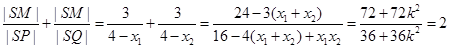

练习册系列答案
相关题目
题目内容
 是椭圆
是椭圆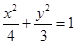 过
过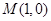 的一动弦,且直线
的一动弦,且直线 与直线
与直线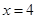 交于点
交于点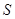 ,则
,则
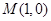 是椭圆的右焦点,直线
是椭圆的右焦点,直线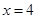 是椭圆的右准线,而
是椭圆的右准线,而 。可知直线
。可知直线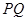 的斜率存在,设其方程为
的斜率存在,设其方程为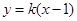 。联立
。联立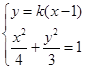 可得
可得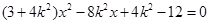 ,设
,设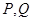 坐标为
坐标为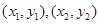 ,则
,则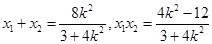 。根据椭圆的第二定义可得,
。根据椭圆的第二定义可得,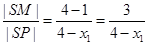 ,
,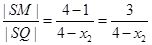 ,所以
,所以