题目内容
已知椭圆的焦点在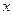 轴上,短轴长为4,离心率为
轴上,短轴长为4,离心率为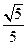 .
.
(1)求椭圆的标准方程;
(2)若直线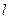 过该椭圆的左焦点,交椭圆于M、N两点,且
过该椭圆的左焦点,交椭圆于M、N两点,且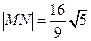 ,求直线
,求直线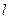 的方程.
的方程.
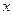 轴上,短轴长为4,离心率为
轴上,短轴长为4,离心率为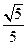 .
. (1)求椭圆的标准方程;
(2)若直线
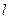 过该椭圆的左焦点,交椭圆于M、N两点,且
过该椭圆的左焦点,交椭圆于M、N两点,且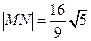 ,求直线
,求直线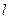 的方程.
的方程.解:(1) 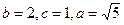 ,椭圆的标准方程:
,椭圆的标准方程: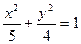
(2)由题意知,直线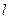 的斜率存在,所以设直线方程为:
的斜率存在,所以设直线方程为: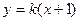 ,
,
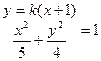 联立得:
联立得:
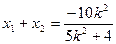 ,
, 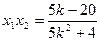
则: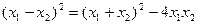
=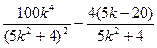 =" "
=" " 
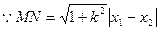
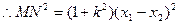
即: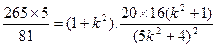
即: ,
,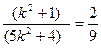
所以, ,所以直线方程为:
,所以直线方程为: 或
或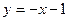
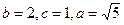 ,椭圆的标准方程:
,椭圆的标准方程: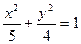
(2)由题意知,直线
 的斜率存在,所以设直线方程为:
的斜率存在,所以设直线方程为: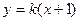 ,
,
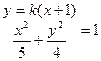 联立得:
联立得:
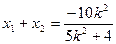 ,
, 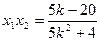
则:
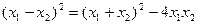
=
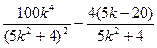 =" "
=" " 
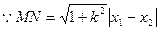
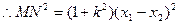
即:
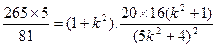
即:
 ,
,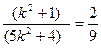
所以,
 ,所以直线方程为:
,所以直线方程为: 或
或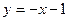
略

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 是椭圆
是椭圆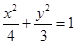 过
过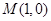 的一动弦,且直线
的一动弦,且直线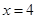 交于点
交于点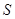 ,则
,则
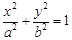 (
(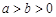 )与双曲线
)与双曲线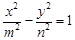 (
(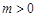 ,
, )有相同的焦点
)有相同的焦点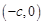 和
和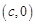 ,若
,若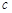 是
是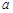 、
、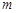 的等比中项,
的等比中项,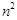 是
是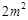 与
与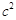 的等差中项,则椭圆的离心率是( )
的等差中项,则椭圆的离心率是( )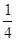

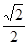

 与曲线
与曲线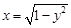 有且仅有一个公共点,则
有且仅有一个公共点,则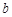 的取值范围是 ( )
的取值范围是 ( )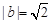
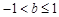 或
或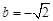

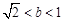
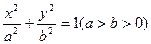 的左右焦点分别为
的左右焦点分别为 ,左顶点为
,左顶点为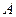 ,若
,若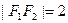 ,椭圆的离心率为
,椭圆的离心率为
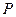 是椭圆上的任意一点,求
是椭圆上的任意一点,求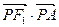 的取值范围
的取值范围 与椭圆相交于不同的两点
与椭圆相交于不同的两点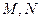 (均不是长轴的顶点),
(均不是长轴的顶点), 垂足为H且
垂足为H且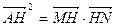 ,求证:直线
,求证:直线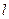 恒过定点.
恒过定点.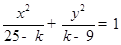 ,则
,则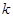 的取值范围为( )
的取值范围为( )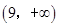
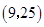
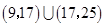
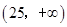
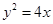 和点
和点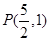 ,过点P的直线
,过点P的直线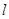 与抛物线交与
与抛物线交与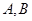 两点,设点P刚好为弦
两点,设点P刚好为弦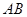 的中点。
的中点。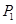 (不含端点
(不含端点 的直线
的直线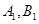 ,类比圆中的相交弦定理,给出你的猜想,若成立,给出证明;若不成立,请说明理由。
,类比圆中的相交弦定理,给出你的猜想,若成立,给出证明;若不成立,请说明理由。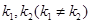 的直线
的直线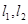 ,
,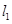 交抛物线于
交抛物线于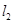 交抛物线于
交抛物线于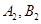 ,是否存在
,是否存在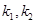 满足的条件。若不存在,请说明理由。
满足的条件。若不存在,请说明理由。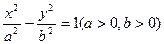 的离心率为
的离心率为 ,且它的一个焦点与抛物线
,且它的一个焦点与抛物线 的焦点重合,则此双曲线的方程__________
的焦点重合,则此双曲线的方程__________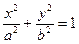 的左右焦点分别为
的左右焦点分别为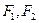 ,P为椭圆上一点,且
,P为椭圆上一点,且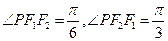 ,则
,则 椭圆的离心率e=________
椭圆的离心率e=________