题目内容
(本小题满分12分)已知定义在正实数集上的函数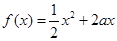 ,
,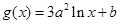 ,其中
,其中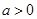 .设两曲线
.设两曲线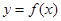 ,
,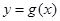 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.
(1)用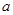 表示
表示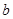 ,并求
,并求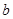 的最大值;
的最大值;
(2)求证: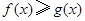 (
(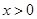 ).
).
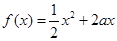 ,
,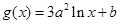 ,其中
,其中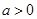 .设两曲线
.设两曲线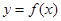 ,
,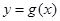 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.(1)用
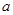 表示
表示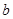 ,并求
,并求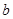 的最大值;
的最大值;(2)求证:
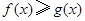 (
(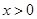 ).
).(1)设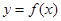 与
与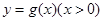 在公共点
在公共点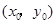 处的切线相同.
处的切线相同.
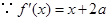 ,
, ,由题意
,由题意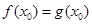 ,
,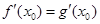 .
.
即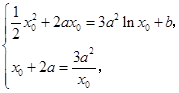 由
由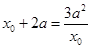
得: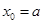 ,或
,或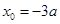 (舍去).
(舍去).
即有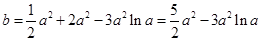 .
.
令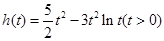 ,则
,则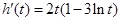 .于是
.于是
当 ,即
,即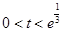 时,
时,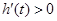 ;
;
当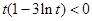 ,即
,即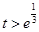 时,
时,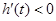 .
.
故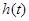 在
在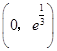 为增函数,
为增函数, 在
在 为减函数,
为减函数,
于是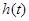 在
在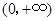 的最大值为
的最大值为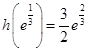 .(2)
.(2)
设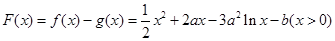 ,
,
则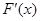
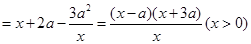 .
.
故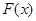 在
在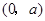 为减函数,在
为减函数,在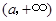 为增函数,
为增函数,
于是函数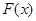 在
在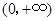 上的最小值是
上的最小值是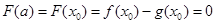 .
.
故当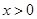 时,有
时,有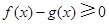 ,即当
,即当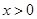 时,
时,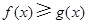
19.经检验,以上所得椭圆的四个顶点无法取到,
故交点轨迹E的方程为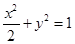
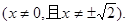
(2)设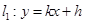
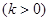 ,则由
,则由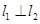 知,
知,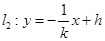 .
.
将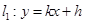 代入
代入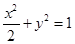 得
得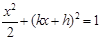 ,
,
即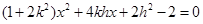 ,
,
若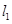 与椭圆相切,则
与椭圆相切,则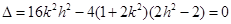 ,即
,即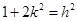 ;
;
同理若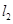 与椭圆相切,则
与椭圆相切,则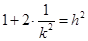 .
.
由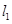 与
与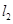 与轨迹E都只有一个交点包含以下四种情况:
与轨迹E都只有一个交点包含以下四种情况:
[1]直线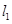 与
与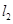 都与椭圆相切,即
都与椭圆相切,即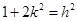 ,且
,且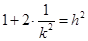 ,消去
,消去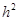 得
得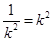 ,即
,即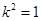 ,
,
从而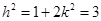 ,即
,即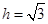 ;
;
[2]直线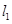 过点
过点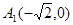 ,而
,而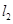 与椭圆相切,此时
与椭圆相切,此时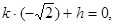
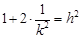 ,解得
,解得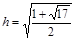 ;
;
[3]直线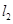 过点
过点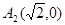 ,而
,而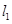 与椭圆相切,此时
与椭圆相切,此时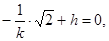
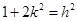 ,解得
,解得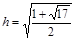 ;
;
[4] 直线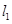 过点
过点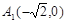 ,而直线
,而直线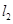 过点
过点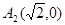 ,此时
,此时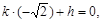
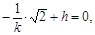
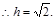
综上所述,h的值为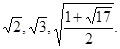
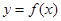 与
与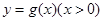 在公共点
在公共点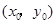 处的切线相同.
处的切线相同.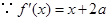 ,
, ,由题意
,由题意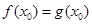 ,
,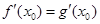 .
.即
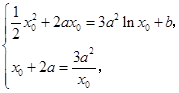 由
由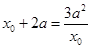
得:
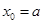 ,或
,或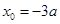 (舍去).
(舍去). 即有
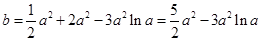 .
.令
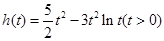 ,则
,则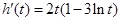 .于是
.于是当
 ,即
,即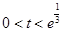 时,
时,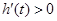 ;
;当
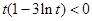 ,即
,即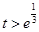 时,
时,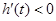 .
.故
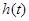 在
在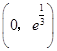 为增函数,
为增函数, 在
在 为减函数,
为减函数,于是
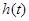 在
在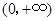 的最大值为
的最大值为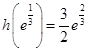 .(2)
.(2)设
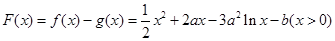 ,
,则
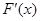
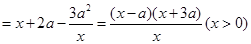 .
.故
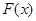 在
在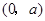 为减函数,在
为减函数,在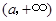 为增函数,
为增函数,于是函数
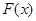 在
在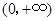 上的最小值是
上的最小值是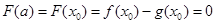 .
.故当
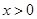 时,有
时,有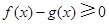 ,即当
,即当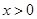 时,
时,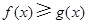
19.经检验,以上所得椭圆的四个顶点无法取到,
故交点轨迹E的方程为
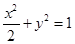
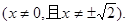
(2)设
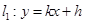
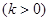 ,则由
,则由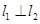 知,
知,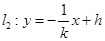 .
.将
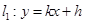 代入
代入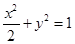 得
得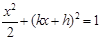 ,
,即
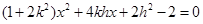 ,
,若
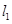 与椭圆相切,则
与椭圆相切,则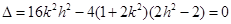 ,即
,即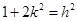 ;
;同理若
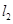 与椭圆相切,则
与椭圆相切,则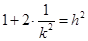 .
.由
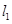 与
与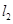 与轨迹E都只有一个交点包含以下四种情况:
与轨迹E都只有一个交点包含以下四种情况:[1]直线
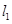 与
与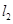 都与椭圆相切,即
都与椭圆相切,即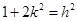 ,且
,且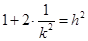 ,消去
,消去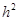 得
得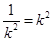 ,即
,即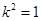 ,
,从而
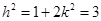 ,即
,即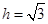 ;
;[2]直线
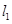 过点
过点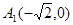 ,而
,而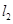 与椭圆相切,此时
与椭圆相切,此时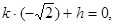
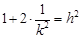 ,解得
,解得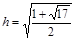 ;
;[3]直线
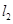 过点
过点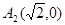 ,而
,而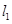 与椭圆相切,此时
与椭圆相切,此时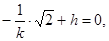
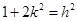 ,解得
,解得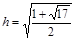 ;
;[4] 直线
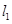 过点
过点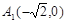 ,而直线
,而直线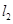 过点
过点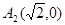 ,此时
,此时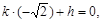
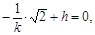
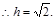
综上所述,h的值为
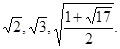
略

练习册系列答案
相关题目
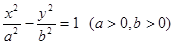 的离心率
的离心率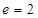 ,右焦点
,右焦点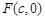 ,方程
,方程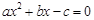 的两个根分别为
的两个根分别为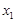 ,
,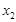 ,则点
,则点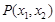 在
在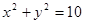 内
内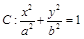
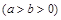 的离心率为
的离心率为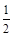 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线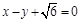 相切.
相切. 的方程;
的方程;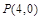 ,
, ,
, 是椭圆
是椭圆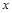 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结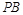 交椭圆
交椭圆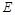 ,证明直线
,证明直线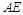 与
与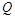 ;
;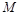 ,
,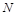 两点,求
两点,求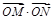 的取值范围.
的取值范围.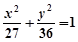 的焦点相同,且它们一个交点的纵坐标为4,则双曲线的虚轴长为
的焦点相同,且它们一个交点的纵坐标为4,则双曲线的虚轴长为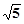
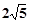
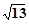
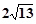
 是椭圆
是椭圆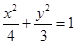 过
过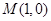 的一动弦,且直线
的一动弦,且直线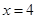 交于点
交于点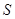 ,则
,则
 ,使得点
,使得点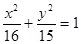
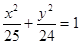
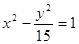
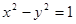
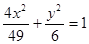 的两个焦点,P是椭圆上的点,且
的两个焦点,P是椭圆上的点,且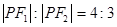 ,则
,则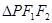 的面积为( )
的面积为( )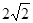
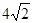
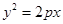 的准线与双曲线
的准线与双曲线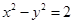 的左准线重合,则p的值为 ▲
的左准线重合,则p的值为 ▲ 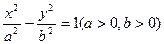 的离心率为
的离心率为 ,且它的一个焦点与抛物线
,且它的一个焦点与抛物线 的焦点重合,则此双曲线的方程__________
的焦点重合,则此双曲线的方程__________