题目内容
已知定点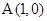 ,定直线
,定直线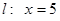 ,动点
,动点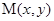
(Ⅰ)、若M到点A的距离与M到直线l的距离之比为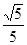 ,试求M的轨迹曲线C1的方程.
,试求M的轨迹曲线C1的方程.
(Ⅱ)、若曲线C2是以C1的焦点为顶点,且以C1的顶点为焦点,试求曲线C2的方程.
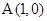 ,定直线
,定直线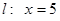 ,动点
,动点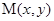
(Ⅰ)、若M到点A的距离与M到直线l的距离之比为
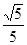 ,试求M的轨迹曲线C1的方程.
,试求M的轨迹曲线C1的方程.(Ⅱ)、若曲线C2是以C1的焦点为顶点,且以C1的顶点为焦点,试求曲线C2的方程.
22、(本小题满分14分)
解:(Ⅰ)、设 是点
是点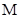 到直线
到直线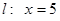 的距离,由题意得:
的距离,由题意得:
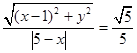 两边平方,并化简,得
两边平方,并化简,得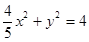
即M的轨迹曲线C1的方程是椭圆: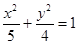 .
.
(Ⅱ)、由题意可知曲线C2是双曲线,设方程为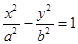
因为椭圆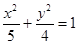 的顶点是(
的顶点是(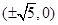 ,焦点是
,焦点是
所以双曲线的顶点是 ,焦点是
,焦点是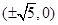 于是
于是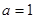 ,
,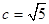
所以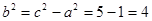 所以曲线C2的方程是
所以曲线C2的方程是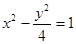
解:(Ⅰ)、设
 是点
是点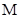 到直线
到直线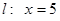 的距离,由题意得:
的距离,由题意得: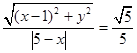 两边平方,并化简,得
两边平方,并化简,得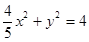
即M的轨迹曲线C1的方程是椭圆:
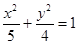 .
.(Ⅱ)、由题意可知曲线C2是双曲线,设方程为
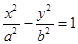
因为椭圆
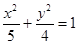 的顶点是(
的顶点是(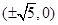 ,焦点是
,焦点是
所以双曲线的顶点是
 ,焦点是
,焦点是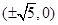 于是
于是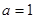 ,
,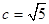
所以
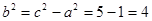 所以曲线C2的方程是
所以曲线C2的方程是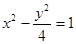
略

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
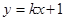 与曲线
与曲线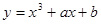 切于点
切于点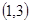 ,则
,则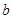 的值为( )
的值为( )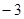
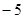
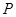 在曲线
在曲线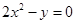 上移动,则点
上移动,则点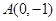 与点
与点 是椭圆
是椭圆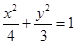 过
过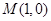 的一动弦,且直线
的一动弦,且直线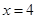 交于点
交于点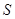 ,则
,则
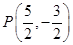 、
、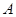 (-2,0)、
(-2,0)、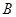 (2,0)。
(2,0)。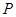 的椭
的椭 圆的标准方程;
圆的标准方程; 的方程为:
的方程为: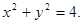 直线
直线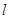 过点
过点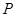 (1,2),且与圆
(1,2),且与圆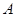 、
、 两点,若
两点,若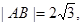 求直线
求直线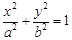 (
(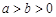 )与双曲线
)与双曲线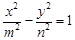 (
(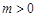 ,
, )有相同的焦点
)有相同的焦点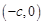 和
和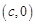 ,若
,若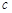 是
是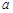 、
、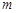 的等比中项,
的等比中项,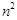 是
是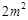 与
与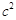 的等差中项,则椭圆的离心率是( )
的等差中项,则椭圆的离心率是( )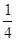

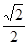

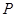 在曲线
在曲线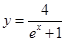 上,
上,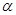 为曲线在点
为曲线在点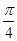 )
)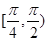
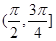
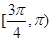
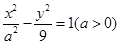 的渐近线方程为
的渐近线方程为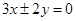 ,则
,则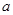 的值为( )
的值为( )