题目内容
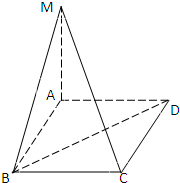
正方形ABCD的边长为a,MA⊥平面ABCD,且MA=a,试求:
(1)点M到BD的距离;
(2)AD到平面MBC的距离.
(1)点M到BD的距离;
(2)AD到平面MBC的距离.

(1)连接AC交BD于O,连接MO.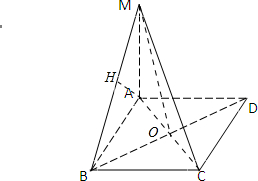
由正方形ABCD可得BD⊥AC.
∵MA⊥平面ABCD,∴MO⊥BD.
∴MO为点M到BD的距离.
∵MA=a,AO=
AC=
a,
∴MO=
=
a2.
2)过A作AH⊥PB于H.
∵MA⊥平面ABCD,BC⊥AB,
∴BC⊥AH.
∵BM∩BC=B.
∴AH⊥平面BCM.
又AD∥BC,AD?平面BCM,BC?平面BCM.
∴AD∥平面BCM.
∴AH为AD到平面MBC的距离.
在Rt△MAB中,AM=
=
a.
∴AH=
=
=
a.
∴AD到平面MBC的距离.

由正方形ABCD可得BD⊥AC.
∵MA⊥平面ABCD,∴MO⊥BD.
∴MO为点M到BD的距离.
∵MA=a,AO=
| 1 |
| 2 |
| ||
| 2 |
∴MO=
| MA2+AO2 |
| ||
| 2 |
2)过A作AH⊥PB于H.
∵MA⊥平面ABCD,BC⊥AB,
∴BC⊥AH.
∵BM∩BC=B.
∴AH⊥平面BCM.
又AD∥BC,AD?平面BCM,BC?平面BCM.
∴AD∥平面BCM.
∴AH为AD到平面MBC的距离.
在Rt△MAB中,AM=
| AM2+AB2 |
| 2 |
∴AH=
| AM•AB |
| BM |
| a2 | ||
|
| ||
| 2 |
∴AD到平面MBC的距离.

练习册系列答案
相关题目
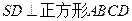 ,
,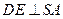 于
于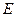 ,
,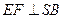 于
于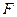 ,
,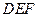 交
交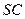 于
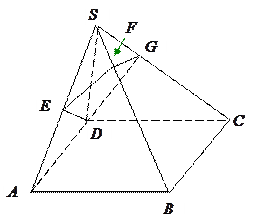
于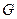 .(1)求证:
.(1)求证: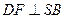 ;(2)求证:
;(2)求证: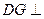 平面
平面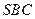 .
.
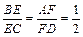 ,EF =
,EF =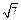 ,则直线AB和CD所成的角的大小是 .
,则直线AB和CD所成的角的大小是 .