题目内容

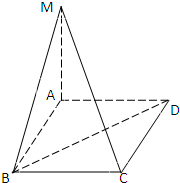
如图，若正方体ABCD-A1B1C1D1的棱长为1，则点C到平面A1BD的距离为______．
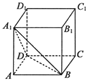
构造三棱锥C-A1DB，并且有Vc-A1BD=VA1-BCD，
因为VA1-BCD=
1
3
sh=
1
3
×
1
2
×1×1×1=
1
6
，
所以Vc-A1BD=
1
6
．
设点C到平面A1BD的距离为x，
又因为Vc-A1BD=
1
3
×SA1BD×x=
3
x
6
=
1
6
，
所以x=
3
3
，即点C到平面A1BD的距离为
3
3
．
故答案为
3
3
．
练习册系列答案
相关题目
正方形ABCD的边长为a，MA⊥平面ABCD，且MA=a，试求：
（1）点M到BD的距离；
（2）AD到平面MBC的距离．
在△ABC中，AB=AC=5，BC=6，PA⊥平面ABC，PA=8，求点P到BC的距离．
如图，棱柱ABC-A1B1C1中，四边形AA1B1B是菱形，四边形BCC1B1是矩形，AB⊥BC，CB=1，AB=2，∠A1AB=60°．
（1）求证：平面CA1B⊥平面A1ABB1；
（2）求B1C1到平面A1CB的距离；
（3）求直线A1C与平面BCC1B1所成角的正切值．
已知矩形的周长为36，矩形绕它的一条边旋转形成一个圆柱，要使旋转形成的圆柱的侧面积最大，则矩形的长为______．
空间四边形ABCD的各边与两条对角线的长都是1，点P在边AB上移动，点Q在CD上移动，则点P与Q的最短距离为（　　）
A．
1
2
B．
2
2
C．
3
4
D．
3
2
以下四个结论：
①若a?α，b?β，则a，b为异面直线；
②若a?α，b?α，则a，b为异面直线；
③没有公共点的两条直线是平行直线；
④两条不平行的直线就一定相交．
其中正确答案的个数是（　　）
A．0个B．1个C．2个D．3个
如图，三棱柱ABC-A1B1C1中，D、E分别是棱BC、AB的中点，点F在棱CC1上，已知AB=AC，AA1=3，BC=CF=2．
（1）求证：C1E∥平面ADF；
（2）若点M在棱BB1上，当BM为何值时，平面CAM⊥平面ADF？
如图，四棱锥P-ABCD的底面ABCD是矩形，AB=2，BC=
2
，且侧面PAB是正三角形，平面PAB⊥平面ABCD，E是棱PA的中点．
（1）求证：PC∥平面EBD；
（2）求三棱锥P-EBD的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网