题目内容
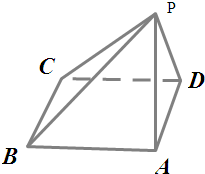
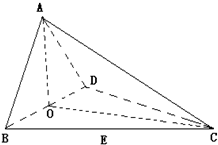
如图四面体ABCD中,O,E分别是BD,BC的中点,CA=CB=CD=BD=2,AB=AD=
(1)求证:直线BD⊥平面AOC
(2)求点E到平面ACD的距离.
| 2 |
(1)求证:直线BD⊥平面AOC
(2)求点E到平面ACD的距离.

(1)证明:连接OC,∵BO=DO,AB=AD,
∴AO⊥BD,
∵BO=DO,BC=CD,∴CO⊥BD.
∵AO⊥BD,CO⊥BD,AO∩OC=O,
∴直线BD⊥平面AOC.(6分)
(2)设点E到平面ACD的距离为h.
∵VE-ACD=VA-CDE,∴
h.S△ACD=
•AO•S△CDE.…(9分)
在△ACD中,CA=CD=2,AD=
,
∴S△ACD=
×
×
=
,
∵AO=1,S△CDE=
×
×22=
,
∴h=
=
=
,
∴点E到平面ACD的距离为
.(6分)
∴AO⊥BD,
∵BO=DO,BC=CD,∴CO⊥BD.
∵AO⊥BD,CO⊥BD,AO∩OC=O,
∴直线BD⊥平面AOC.(6分)
(2)设点E到平面ACD的距离为h.
∵VE-ACD=VA-CDE,∴
| 1 |
| 3 |
| 1 |
| 3 |
在△ACD中,CA=CD=2,AD=
| 2 |
∴S△ACD=
| 1 |
| 2 |
| 2 |
4-(
|
| ||
| 2 |
∵AO=1,S△CDE=
| 1 |
| 2 |
| ||
| 4 |
| ||
| 2 |
∴h=
| AO•S△CDE |
| S△ACD |
1×
| ||||
|
| ||
| 7 |
∴点E到平面ACD的距离为
| ||
| 7 |

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目

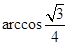
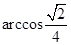
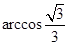
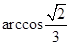
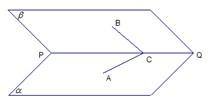
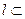 平面
平面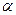 ,过平面
,过平面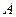 与
与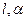 都成
都成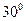 角的直线有且只有( )
角的直线有且只有( )