题目内容
已知空间四边形ABCD中,AB = CD = 3,E、F分别为BC、AD上的点,且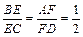 ,EF =
,EF =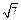 ,则直线AB和CD所成的角的大小是 .
,则直线AB和CD所成的角的大小是 .
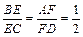 ,EF =
,EF =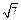 ,则直线AB和CD所成的角的大小是 .
,则直线AB和CD所成的角的大小是 .60°
作FH∥AB交BD于H,则 ,∴
,∴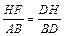 ,∴HF =
,∴HF = 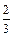 AB = 2,在△HEF中
AB = 2,在△HEF中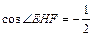 ,∴∠EHF的补角60°为AB、CD所成角.
,∴∠EHF的补角60°为AB、CD所成角.
 ,∴
,∴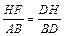 ,∴HF =
,∴HF = 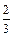 AB = 2,在△HEF中
AB = 2,在△HEF中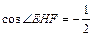 ,∴∠EHF的补角60°为AB、CD所成角.
,∴∠EHF的补角60°为AB、CD所成角.
练习册系列答案
相关题目

 SA=AB,AB⊥BC,SB=BC,E是SC的中点,
SA=AB,AB⊥BC,SB=BC,E是SC的中点,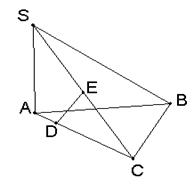
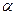 ,
,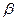 ,直线
,直线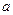 满足
满足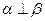 ,
,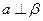 ,
,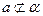 ,试判断直线
,试判断直线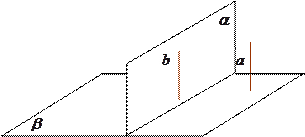
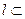 平面
平面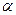 ,过平面
,过平面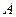 与
与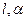 都成
都成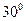 角的直线有且只有( )
角的直线有且只有( )