题目内容
7．已知命题p：若$\overrightarrow{a}$是非零向量，λ是非零实数，则$\overrightarrow{a}$与-λ$\overrightarrow{a}$方向相反；命题q：|-λ$\overrightarrow{a}$|=|λ|•$\overrightarrow{a}$．则下列命题为真命题的是（ ）| A． | p∧q | B． | p∨q | C． | （￢p）∨q | D． | p∧（￢q） |
分析 对于命题p：若$\overrightarrow{a}$是非零向量，λ是非零实数，则$\overrightarrow{a}$与-λ$\overrightarrow{a}$方向相反或相同，是假命题；对于命题q：应该有|-λ$\overrightarrow{a}$|=|λ|•|$\overrightarrow{a}$|，因此是假命题．即可判断出真假．
解答 解：命题p：若$\overrightarrow{a}$是非零向量，λ是非零实数，则$\overrightarrow{a}$与-λ$\overrightarrow{a}$方向相反或相同，是假命题；
命题q：|-λ$\overrightarrow{a}$|=|λ|•|$\overrightarrow{a}$|，因此是假命题．
∴￢p是真命题，（￢p）∨q是真命题，p∧q，p∨q，p∧（￢q）是假命题．
故选：C．
点评 本题考查了复合命题真假的判定方法，考查了推理能力，属于基础题．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
如图，四边形ABCD为平行四边形，AB=5，AD=4，BD=3，将△BCD沿着BD翻折到平面BC1D处（不与平面ABCD重合），E，F分别为对边AB，C1D的中点，
15．已知△ABC中，角A，B，C所对的边分别为a，b，c，且b+c=8，1+$\frac{tanA}{tanB}$=$\frac{2c}{b}$，则△ABC面积的最大值为（ ）
| A． | 4 | B． | 4$\sqrt{3}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{1}{2}$ |
2．在区域$\left\{\begin{array}{l}0≤x≤1\\ 0≤y≤1\end{array}\right.$内任意取一点P（x，y），则x2+y2＞1的概率是（ ）
| A． | $\frac{2π-4}{4}$ | B． | $\frac{π-2}{4}$ | C． | $\frac{π}{4}$ | D． | $\frac{4-π}{4}$ |
19．
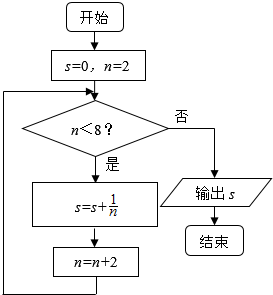如图所示，程序框图的输出结果是（ ）
如图所示，程序框图的输出结果是（ ）| A． | $\frac{1}{16}$ | B． | $\frac{25}{24}$ | C． | $\frac{11}{12}$ | D． | $\frac{3}{4}$ |
将5个全等的正方形按如图所示方式放置在一个的矩形OEFG内，其中顶点P、C、Q、D分别在矩形的四条边上．