题目内容
18.计算:∫1−1|1-x|dx=2.分析 首先根据x范围去掉绝对值,然后找出被积函数的原函数计算定积分.
解答 解:原式=∫1−1(1−x)dx=(x-12x2)|1−1=2.
故答案为:2.
点评 本题考查了定积分的求法;关键是去掉绝对值,求出被积函数的原函数.

练习册系列答案
相关题目
5.12−sin225°cos20°•cos70°=( )
| A. | √34 | B. | √32 | C. | 12 | D. | 1 |
7.已知命题p:若→a是非零向量,λ是非零实数,则→a与-λ→a方向相反;命题q:|-λ→a|=|λ|•→a.则下列命题为真命题的是( )
| A. | p∧q | B. | p∨q | C. | (¬p)∨q | D. | p∧(¬q) |
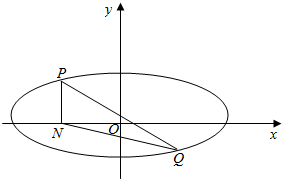 已知椭圆C:
已知椭圆C: