题目内容
14. 如图,四边形ABCD为平行四边形,AB=5,AD=4,BD=3,将△BCD沿着BD翻折到平面BC1D处(不与平面ABCD重合),E,F分别为对边AB,C1D的中点,
如图,四边形ABCD为平行四边形,AB=5,AD=4,BD=3,将△BCD沿着BD翻折到平面BC1D处(不与平面ABCD重合),E,F分别为对边AB,C1D的中点,(Ⅰ)求证:EF⊥BD;
(Ⅱ)若异面直线EF,BC1所成的角为30°,求二面角C1-AB-D的平面角的正切值.
分析 (Ⅰ)连结CC1,并取CC1的中点M,连结FM,BM,证明BD⊥平面BCC1,即可证明:EF⊥BD;
(Ⅱ)取BC的中点N,过N作线段AB的垂线交AB的延长线于点H.由(Ⅰ)知,异面直线EF,BC1所成的角为∠C1BM,故∠C1BM=30°,证明∠C1HN为二面角C1-AB-D的平面角,即可求二面角C1-AB-D的平面角的正切值.
解答 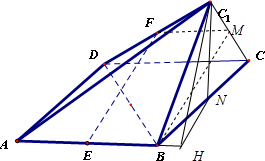 (Ⅰ)证明:连结CC1,并取CC1的中点M,连结FM,BM.
(Ⅰ)证明:连结CC1,并取CC1的中点M,连结FM,BM.
因为F分别为C1D的中点,所以,FM∥DC且FM=$\frac{1}{2}$DC;
因为四边形ABCD为平行四边形,所以,DC∥AB,DC=AB;
又E分别为AB的中点,所以,FM∥EB,FM=EB,
即四边形FMDE为平行四边形;…(3分)
所以,EF∥MB.
因为AB=5,AD=4,BD=3,;
所以,BD⊥AD,BD⊥BC,BD⊥BC1;
所以,BD⊥平面BCC1.
又因为BM?平面BCC1,所以BD⊥BM,BD⊥EF.…(6分)
(Ⅱ)解:取BC的中点N,过N作线段AB的垂线交AB的延长线于点H.
由(Ⅰ)知,异面直线EF,BC1所成的角为∠C1BM,故∠C1BM=30°;
因为BC=BC1,M为CC1的中点,所以,∠C1BC=60°,即△C1BC为正三角形.
所以C1N⊥BC.…(9分)
又BD⊥平面BCC1,所以,平面ABCD⊥平面BCC1;
因为平面ABCD∩平面BCC1=BC,
所以C1N⊥平面ABCD,所以C1N⊥AB;
所以,∠C1HN为二面角C1-AB-D的平面角.…(12分)
在Rt△C1NH中,C1N=$\frac{\sqrt{3}}{2}$BC=2$\sqrt{3}$,NH=NB•sin∠NBH=$\frac{1}{2}$BC•$\frac{BD}{AB}$=$\frac{6}{5}$,
所以,tan∠C1HN=$\frac{{C}_{1}N}{NH}$=$\frac{5\sqrt{3}}{3}$,
即二面角C1-AB-D的平面角的正切值为$\frac{5\sqrt{3}}{3}$.…(15分)
点评 本题考查线面垂直的判定与性质,考查线面角,二面角的平面角,考查学生分析解决问题的能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
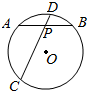 如图,在半径为$\sqrt{7}$的⊙O中,弦AB、CD相交于点P,PA=PB=2,PD=1.
如图,在半径为$\sqrt{7}$的⊙O中,弦AB、CD相交于点P,PA=PB=2,PD=1. 函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0,0<φ<π)的图象如图所示,则A=2,ω=2,F($\frac{π}{3}$)=1.
函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0,0<φ<π)的图象如图所示,则A=2,ω=2,F($\frac{π}{3}$)=1.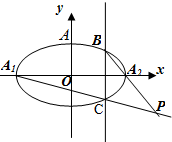 如图已知椭圆G:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,设A(0,b),若△AF1F2为正三角形且周长为6.
如图已知椭圆G:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,设A(0,b),若△AF1F2为正三角形且周长为6.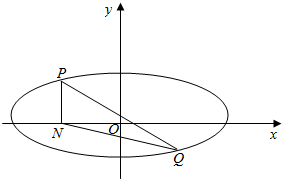 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,且椭圆C经过点(0,1).
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,且椭圆C经过点(0,1).