题目内容
17. 将5个全等的正方形按如图所示方式放置在一个的矩形OEFG内,其中顶点P、C、Q、D分别在矩形的四条边上.
将5个全等的正方形按如图所示方式放置在一个的矩形OEFG内,其中顶点P、C、Q、D分别在矩形的四条边上.(1)设向量$\overrightarrow{PA}$=a,$\overrightarrow{PB}$=b,以向量a,b为基底,则向量$\overrightarrow{CD}$=3b-2a(用向量a,b表示);
(2)若OE=7,OG=8,则图中5个正方形的边长都为$\sqrt{5}$.
分析 (1)把要求的向量表示成以小正方形的边为向量的形式,得到的关于正方形边的式子,得到结果.
(2)建立直角坐标系,用x、y表示出$\overrightarrow{PA}$、$\overrightarrow{PB}$,在表示出含有OE、OG的向量,联立方程组解出答案即可.
解答 解: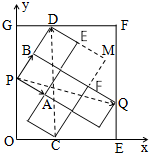 (1)由图可知,做点E、F,
(1)由图可知,做点E、F,
延长DE、CF,交于点M;
∴$\overrightarrow{CD}=\overrightarrow{CM}+\overrightarrow{MD}$=$3\overrightarrow{PB}-2\overrightarrow{PA}$=3b-2a;
(2)如图所示建立直角坐标系,连接PQ;
设$\overrightarrow{PA}=(x,y)$,则$\overrightarrow{PB}=(-y,x)$;
∴$\overrightarrow{CD}$=3b-2a=(-2x-3y,3x-2y);
$\overrightarrow{PQ}$=3a+b=(3x-y,x+3y);
∵OE=7,OG=8,则$\left\{\begin{array}{l}{3x-y=7}\\{3x-2y=8}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$;
∴$|\overrightarrow{PA}|=\sqrt{{x^2}+{y^2}}=\sqrt{5}$,
即正方形的边长为$\sqrt{5}$.
点评 本题考查向量的基本定理,这种问题解起来方向非常明确,只要把要用的向量写成已知条件比较多的正方形的边的形式就可以.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.已知命题p:若$\overrightarrow{a}$是非零向量,λ是非零实数,则$\overrightarrow{a}$与-λ$\overrightarrow{a}$方向相反;命题q:|-λ$\overrightarrow{a}$|=|λ|•$\overrightarrow{a}$.则下列命题为真命题的是( )
| A. | p∧q | B. | p∨q | C. | (¬p)∨q | D. | p∧(¬q) |
7.“α为第一象限角”是“$\frac{sinα}{cosα}$+$\frac{cosα}{sinα}$≥2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |